Закон Ципфа

Материал из wikixw
Перейти к навигации Перейти к поиску

Закон лингвистики о длине слова см. В Закон аббревиатуры Зипфа.

Закон Ципфа (/зɪф/, а не /тсɪпф/ а на немецком языке) - это эмпирический закон , сформулированный с помощью математической статистики , что указывает на то, что многие типы данных, изученных в физических и социальных науках могут быть аппроксимированы Zipfian распределения, одна из семьи, связанных с дискретной степенной закон распределения вероятностей. Распределение Zipf связано с Дзета-распределением, но не идентично ему.

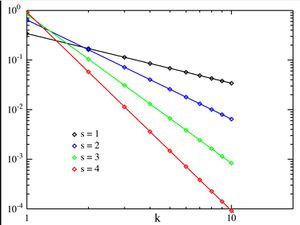
Zipf PMF для N = 10 по логарифмической шкале. Горизонтальная ось - это индекс к. (Обратите внимание, что функция определяется только при целочисленных значениях k. Соединительные линии не указывают на непрерывность.)

Закон зипфа был первоначально сформулирован в терминах количественной лингвистики, утверждая, что при наличии некоторого корпуса высказываний естественного языка частота любого слова обратно пропорциональна его рангу в таблице частот. Таким образом, наиболее частое слово будет встречаться примерно в два раза чаще, чем второе наиболее частое слово, в три раза чаще, чем третье наиболее частое слово и т. д.: рангово-частотное распределение является обратной зависимостью. Например, в коричневом корпусе американского английского текста слово the это наиболее часто встречающееся слово, и само по себе составляет почти 7% всех встречающихся слов (69 971 из чуть более 1 миллиона). Согласно закону Зипфа, на второе место приходится чуть более 3,5% слов (36 411 вхождений), за ними следует и (28 852). Только 135 словарных единиц необходимы, чтобы учесть половину коричневого корпуса.

Закон назван в честь американского лингвиста Джорджа Кингсли Зипфа (1902-1950), который популяризировал его и пытался объяснить (Zipf 1935, 1949), хотя и не утверждал, что он был его автором.Французский стенограф Жан-Батист Эступ (1868-1950), по-видимому, заметил эту закономерность еще до Зипфа.[не проверено в теле] это было также отмечено в 1913 году немецким физиком Феликсом Ауэрбахом (1856-1933).

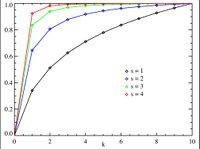
Zipf CDF для N = 10. Горизонтальная ось - это индекс к. (Обратите внимание, что функция определяется только при целочисленных значениях k. Соединительные линии не указывают на непрерывность.)

Другие наборы данных[править]

оп

Такое же отношение возникает и во многих других рейтингах человека созданы системы, такие как ряды математических выражений[6] или ряды нот в музыке, и даже в неконтролируемых средах, таких как население рядах городов в разных странах, размеры корпорации, доходы, рейтинги, звания кол-во человек смотрит один и тот же ТВ канал, и так далее. Появление распределения в рейтингах городов по населению впервые было замечено Феликсом Ауэрбахом в 1913 году. Эмпирически набор данных можно проверить, применим ли закон Зипфа, проверив правильность соответствия эмпирического распределения гипотетическому распределению степенного закона с помощью критерия Колмогорова-Смирнова, а затем сравнив (логарифмическое) отношение правдоподобия распределения степенного закона с альтернативными распределениями, такими как экспоненциальное распределение или логнормальное распределение. при проверке закона Зипфа для городов было найдено лучшее соответствие с показателем s = 1,07; то есть самое n t h }большое поселение-это 1 n 1.07 }}размер самого большого поселения.

Теоретический обзор[править]

Закон зипфа легче всего наблюдать, построив данные на логарифмическом графике, осями которого являются log (порядок рангов) и log (частота). Например, слово " the " (как описано выше) появится в X = log(1), y = log (69971). Также можно построить взаимный ранг против частоты или взаимную частоту или межсловный интервал против ранга.[2] данные соответствуют закону Зипфа в той мере, в какой график является линейным.

Формально, пусть:

  1. N-число элементов;
  2. k быть их рангом;
  3. s - значение показателя, характеризующего распределение.

Затем закон зипфа предсказывает, что из совокупности N элементов нормированная частота элементов ранга k, f(k;s,N), равна: 

   f ( k ; s , N ) = 1 / k s ∑ n = 1 N ( 1 / n s )

Закон зипфа справедлив, если число элементов с заданной частотой является случайной величиной с степенным законом распределения p ( f ) = α f − 1 − 1 / s .

Было заявлено, что это представление закона Зипфа более подходит для статистической проверки, и таким образом оно было проанализировано в более чем 30 000 английских текстах. Тесты на соответствие требованиям показывают, что только около 15% текстов статистически совместимы с этой формой закона Зипфа. Незначительные изменения в определении закона Зипфа могут увеличить этот процент почти до 50%.

В Примере частоты слов в английском языке N - это число слов в английском языке, и, если мы используем классическую версию закона Зипфа, показатель s равен 1. f(k; s,N) будет тогда долей времени, в течение которого встречается k-е наиболее распространенное слово.

Закон также может быть написан: 

   f ( k ; s , N ) = 1 k s H N , s {

где HN, s-N-е обобщенное гармоническое число.

Простейшим случаем закона Зипфа является функция "1/f"."Учитывая набор распределенных частот Zipfian, отсортированных от наиболее распространенных до наименее распространенных, вторая наиболее распространенная частота будет возникать вдвое чаще первой, третья наиболее распространенная частота будет возникать 1/3 так же часто, как первая, и n-я наиболее распространенная частота будет возникать 1/n так же часто, как и в первый раз. Однако это не может быть выполнено точно, потому что элементы должны встречаться целое число раз; не может быть 2,5 вхождения слова. Тем не менее, в довольно широких пределах и в довольно хорошем приближении многие природные явления подчиняются закону Зипфа.

В человеческих языках частоты слов имеют очень тяжелое хвостатое распределение и поэтому могут быть достаточно хорошо смоделированы распределением Zipf с s, близким к 1.

Пока показатель степени s превышает 1, такой закон может выполняться с бесконечным числом слов, так как если s > 1, то 

   ζ ( s ) = ∑ n = 1 ∞ 1 n s < ∞ . \!

где ζ-Дзета-функцияРимана .

Статистическое объяснение[править]

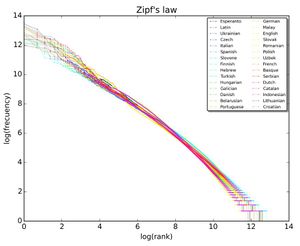
График зависимости ранга от частоты для первых 10 миллионов слов в 30 Википедиях (дампы с октября 2015 года) в логарифмической шкале.

Хотя закон Зипфа применим ко всем языкам, даже к таким неестественным, как эсперанто, причина этого все еще не вполне понятна. однако это может быть частично объяснено статистическим анализом случайно сгенерированных текстов. Вэньтянь Ли показал, что в документе, в котором каждый символ был выбран случайным образом из равномерного распределения всех букв (плюс пробел), "слова" с разной длиной следуют макротренду закона Зипфа (наиболее вероятные слова являются самыми короткими с равной вероятностью). Витольд Белевич в газете, По статистическим законам лингвистического распределения предложен математический вывод. Он взял большой класс хорошо управляемых статистических распределений (не только нормальное распределение) и выразил их в терминах ранга. Затем он расширил каждое выражение в ряд Тейлора. В каждом случае Белевич получал замечательный результат: усечение ряда первого порядка приводило к закону Зипфа. Далее, усечение второго порядка ряда Тейлора привело к закону Мандельброта.

Другим возможным объяснением является принцип наименьшего усилия: Сам зипф предположил, что ни говорящие, ни слушатели, использующие данный язык, не хотят работать больше, чем необходимо для достижения понимания, и процесс, который приводит к приблизительно равному распределению усилий, приводит к наблюдаемому распределению Зипфа.

Точно так же было показано, что предпочтительная привязанность (интуитивно "богатые становятся богаче" или "успех порождает успех"), которая приводит к распределению Юла–Саймона, соответствует частоте слов в сравнении с рангом в языке и населению в сравнении с рангом города лучше, чем закон Зипфа. Первоначально он был выведен для объяснения соотношения численности и ранга видов Юлом и применен к городам Саймоном.

Связанные с этим законы[править]

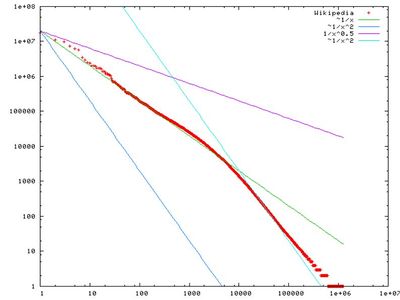
График частотности слов в Википедии (27 ноября 2006 года). Участок находится в логарифмических координатах. x-ранг слова в таблице частот; y-общее число вхождений слова. Самые популярные слова - "the", "of" И "and", как и ожидалось. Закон зипфа соответствует средней линейной части кривой, приблизительно следующей за зеленой (1/x) линией, в то время как ранняя часть ближе к пурпурной (1/x0,5) линии, а более поздняя часть ближе к Голубой( 1/ (k + x)2,0) линии. Эти линии соответствуют трем различным параметризациям распределения Зипфа-Мандельброта, в целом a нарушен закон силы с тремя сегментами: головой, серединой и хвостом.

Закон зипфа на самом деле относится более широко к частотным распределениям "ранговых данных", в которых относительная частота n-го рангового элемента задается Дзета-распределением, 1/(nsζ(s)), где параметр s > 1 индексирует члены этого семейства вероятностных распределений. Действительно, закон Зипфа иногда синонимичен "Дзета-распределению", поскольку распределения вероятностей иногда называют"законами". Это распределение иногда называют зипфианским распределением.

Обобщением закона Зипфа является закон Зипфа-Мандельброта, предложенный БенуаМандельбротом, частоты которого равны: 

   f ( k ; N , q , s ) = [ constant ] ( k + q ) s .

"Константа" является обратной величиной дзета-функции Гурвица, оцениваемой в точке s. На практике, как легко наблюдаемые в распределении участков для больших корпусов, наблюдаемое распределение можно моделировать точнее как сумма отдельных дистрибутивов для разных подмножеств или подтипы слов, которые следуют различные параметризации Zipf–Мандельброта распределения, в частности, закрыты класса функциональной слов экспонат ы ниже, чем 1, в то время как открытые лексики рост с размер документа и размер корпуса требуют с больше чем 1 для сходимости обобщенного гармонического ряда.

Распределения зипфа могут быть получены из распределений Парето путем обмена переменными.

Распределение Zipf иногда называют дискретным распределением Парето, поскольку оно аналогично непрерывному распределению Парето точно так же, как дискретное равномерное распределение аналогично непрерывному равномерному распределению.

Хвостовые частоты распределения Юла-Саймона приблизительно равны 

   f ( k ; ρ ) ≈ [ constant ] k ρ + 1 {

для любого выбора ρ > 0.

В параболическом фрактальном распределениилогарифм частоты является квадратичным полиномом логарифма ранга. Это может заметно улучшить подгонку по сравнению с простыми степенными отношениями. Как и фрактальная размерность, можно вычислить размерность Zipf, которая является полезным параметром при анализе текстов.

Было доказано, что закон Бенфорда является частным ограниченным случаем закона Ципфа, причем связь между этими двумя законами объясняется тем, что оба они происходят из масштабно-инвариантных функциональных отношений статистической физики и критических явлений.Соотношения вероятностей в законе Бенфорда не являются постоянными. Начальные цифры данных, удовлетворяющих закону Зипфа при s = 1, удовлетворяют закону Бенфорда.

оп

Приложения[править]

В теории информациисимвол (событие, сигнал) вероятности p псодержит − log 2 ⁡ ( 1 / p ) } биты информации. Следовательно, закон Зипфа для натуральных чисел: Pr ( x ) ≈ 1 / x }эквивалентен числу x икс, содержащему log 2 ⁡ ( x ) биты информации. Чтобы добавить информацию из символа вероятности p пв информацию, уже хранящуюся в натуральном числе x икс, мы должны перейти к x ′ } x'такому, что log 2 ⁡ ( x ′ ) ≈ log 2 ⁡ ( x ) + log 2 ⁡ ( 1 / p ) , или эквивалентно x ′ ≈ x / p }. Например , в стандартной двоичной системе мы имеем x ′ = 2 x + s то, что оптимально для Pr ( s = 0 ) = Pr ( s = 1 ) = 1 / 2 }распределения вероятностей. x ′ ≈ x / p }Правило использования для общего распределения вероятностей лежит в основе семейства асимметричных систем счисления методов энтропийного кодирования используемых при сжатии данных, государственное распределение которого также регулируется законом Zipf.

Закон зипфа также использовался для извлечения параллельных фрагментов текстов из сопоставимых корпусов.

См. также[править]

Дальнейшее чтение[править]

Первичный:

  • Зипф (1949) человеческое поведение и принцип наименьших усилий . Эддисон-Уэсли. "Текст онлайн [1]"
  • Зипф (1935) Психобиология языка . Хоутон-Миффлин.

Вторичный:

/papers.ssrn.com/sol3/papers.cfm?abstract_id=2918642

Пруф[править]

/terrytao.wordpress.com/2009/07/03/benfords-law-zipfs-law-and-the-pareto-distribution/

Источник — https://wikixw.ru/index.php?title=Закон_Ципфа&oldid=18430