Тетраэдр: различия между версиями
Нет описания правки |
|||
| (не показаны 24 промежуточные версии этого же участника) | |||
| Строка 7: | Строка 7: | ||
Тетраэдр - это один из видов пирамиды, представляющий собой многогранник с плоским многоугольным основанием и треугольными гранями, соединяющими основание с общей точкой. В случае тетраэдра основанием является треугольник (основанием может считаться любая из четырех граней), поэтому тетраэдр также известен как "треугольная пирамида". | Тетраэдр - это один из видов пирамиды, представляющий собой многогранник с плоским многоугольным основанием и треугольными гранями, соединяющими основание с общей точкой. В случае тетраэдра основанием является треугольник (основанием может считаться любая из четырех граней), поэтому тетраэдр также известен как "треугольная пирамида". | ||
Как и все выпуклые многогранники, тетраэдр можно сложить из одного листа бумаги. Он имеет две такие сетки. | Как и все выпуклые многогранники, тетраэдр можно сложить из одного листа бумаги. Он имеет две такие сетки. | ||
Для любого тетраэдра существует сфера (называемая окружностью), на которой лежат все четыре вершины, и другая сфера (внутренняя сфера), касательная к граням тетраэдра. | Для любого тетраэдра существует сфера (называемая окружностью), на которой лежат все четыре вершины, и другая сфера (внутренняя сфера), касательная к граням тетраэдра. | ||
Тетраэдр - энергия [[ Огонь|огня]]. | |||
[[Файл:Tetrahedron.gif|100px|thumb|right|[[Тетраэдр]] ]] | [[Файл:Tetrahedron.gif|100px|thumb|right|[[Тетраэдр]] ]] | ||
[[Файл:Тетрард-27.png|200px|thumb|right|]] | |||
==Правильный тетраэдр== | ==Правильный тетраэдр== | ||
Правильный тетраэдр - это тетраэдр, все четыре грани которого являются равносторонними треугольниками. Это одно из пяти правильных платоновых тел, которые были известны с древности. | Правильный тетраэдр - это тетраэдр, все четыре грани которого являются равносторонними треугольниками. Это одно из пяти правильных платоновых тел, которые были известны с древности. | ||
| Строка 70: | Строка 74: | ||
===Ортогональные проекции правильного тетраэдра=== | ===Ортогональные проекции правильного тетраэдра=== | ||
[[Файл:Ortdka4-11.png|400px|thumb| | [[Файл:Ortdka4-11.png|400px|thumb|centre|]] | ||
Правильный тетраэдр имеет две специальные ортогональные проекции, одна из которых центрирована на вершине или, что эквивалентно, на грани, а другая центрирована на ребре. Первый соответствует плоскости Кокстера А2 | Правильный тетраэдр имеет две специальные ортогональные проекции, одна из которых центрирована на вершине или, что эквивалентно, на грани, а другая центрирована на ребре. Первый соответствует плоскости Кокстера А2 | ||
===Поперечное сечение правильного тетраэдра=== | ===Поперечное сечение правильного тетраэдра=== | ||
[[Файл:Regular tetrahedron square cross section.png| | [[Файл:Regular tetrahedron square cross section.png|200px|thumb|right|Центральное поперечное сечение правильного тетраэдра представляет собой квадрат.]] | ||
[[Файл:Tetragonal disphenoid diagram.png|400px|thumb| | [[Файл:Tetragonal disphenoid diagram.png|400px|thumb|left|Тетрагональный дисфеноид, рассматриваемый ортогонально двум зеленым краям.]] | ||
Два косо перпендикулярных противоположных ребра правильного тетраэдра определяют набор параллельных плоскостей. Когда одна из этих плоскостей пересекает тетраэдр, результирующее поперечное сечение представляет собой прямоугольник.[7] Когда пересекающаяся плоскость находится вблизи одного из ребер, прямоугольник длинный и узкий. На полпути между двумя ребрами пересечение представляет собой квадрат. Соотношение сторон прямоугольника меняется на противоположное, когда вы проходите эту промежуточную точку. Для пересечения средней точки квадрата результирующая граничная линия пересекает каждую грань тетраэдра аналогичным образом. Если тетраэдр разделить пополам в этой плоскости, обе половины станут клиньями. | Два косо перпендикулярных противоположных ребра правильного тетраэдра определяют набор параллельных плоскостей. Когда одна из этих плоскостей пересекает тетраэдр, результирующее поперечное сечение представляет собой прямоугольник.[7] Когда пересекающаяся плоскость находится вблизи одного из ребер, прямоугольник длинный и узкий. На полпути между двумя ребрами пересечение представляет собой квадрат. Соотношение сторон прямоугольника меняется на противоположное, когда вы проходите эту промежуточную точку. Для пересечения средней точки квадрата результирующая граничная линия пересекает каждую грань тетраэдра аналогичным образом. Если тетраэдр разделить пополам в этой плоскости, обе половины станут клиньями. | ||
| Строка 82: | Строка 86: | ||
===Сферическая черепица=== | ===Сферическая черепица=== | ||
[[Файл:Cherpc8-05.png| | [[Файл:Cherpc8-05.png|200px|thumb|left|Ортогональная проекция Стереографическая проекция]] | ||
Тетраэдр также может быть представлен в виде сферической плитки и спроецирован на плоскость с помощью стереографической проекции. Эта проекция является конформной, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружности. | Тетраэдр также может быть представлен в виде сферической плитки и спроецирован на плоскость с помощью стереографической проекции. Эта проекция является конформной, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружности. | ||
===Спиральная укладка=== | ===Спиральная укладка=== | ||
[[Файл:600-cell tet ring.png| | [[Файл:600-cell tet ring.png|200px|thumb|right|Одиночный 30-тетраэдрический кольцевой спираль Бурдейка–Кокстера в пределах 600 ячеек, видимый в стереографической проекции]] | ||
Правильные тетраэдры могут быть сложены лицом к лицу в киральную апериодическую цепь, называемую спиралью Бурдейка–Кокстера. | Правильные тетраэдры могут быть сложены лицом к лицу в киральную апериодическую цепь, называемую спиралью Бурдейка–Кокстера. | ||
| Строка 94: | Строка 98: | ||
==Неправильные тетраэдры== | ==Неправильные тетраэдры== | ||
[[Файл:Tetrahedral subgroup tree.png|400px|thumb| | [[Файл:Tetrahedral subgroup tree.png|400px|thumb|left|Отношения подгрупп тетраэдрической симметрии]] | ||
[[Файл:Tetrahedron symmetry tree.png|400px|thumb| | [[Файл:Tetrahedron symmetry tree.png|400px|thumb|centre|Тетраэдрические симметрии, показанные на тетраэдрических диаграммах]] | ||
Тетраэдры, у которых нет четырех равносторонних граней, классифицируются и называются по симметриям, которыми они обладают. | Тетраэдры, у которых нет четырех равносторонних граней, классифицируются и называются по симметриям, которыми они обладают. | ||
| Строка 116: | Строка 120: | ||
===Дисфеноид=== | ===Дисфеноид=== | ||
Основная статья: [[Дисфеноид]] | Основная статья: [[Дисфеноид]] | ||
[[Файл:Oblate tetrahedrille cell.png| | [[Файл:Oblate tetrahedrille cell.png|200px|thumb|left|Тетраэдрический дисфеноид, заполняющий пространство внутри куба. Два ребра имеют двугранные углы 90 °, а четыре ребра имеют двугранные углы 60 °.]] | ||
Дисфеноид - это тетраэдр с четырьмя соответствующими треугольниками в качестве граней; треугольники обязательно имеют все острые углы. Правильный тетраэдр является частным случаем дисфеноида. Другие названия той же формы включают бисфеноид, равнобедренный тетраэдр и равнобедренный тетраэдр. | Дисфеноид - это тетраэдр с четырьмя соответствующими треугольниками в качестве граней; треугольники обязательно имеют все острые углы. Правильный тетраэдр является частным случаем дисфеноида. Другие названия той же формы включают бисфеноид, равнобедренный тетраэдр и равнобедренный тетраэдр. | ||
| Строка 305: | Строка 309: | ||
==Связанные многогранники и соединения== | ==Связанные многогранники и соединения== | ||
[[Файл:Svyazn-12.png| | [[Файл:Svyazn-12.png|600px|thumb|centre|]] | ||
Правильный тетраэдр можно рассматривать как вырожденный многогранник, однородную дигональную антипризму, где базовые многоугольники являются редуцированными дигонами. | Правильный тетраэдр можно рассматривать как вырожденный многогранник, однородную дигональную антипризму, где базовые многоугольники являются редуцированными дигонами. | ||
[[Файл: | [[Файл:Антипризм-22.png|600px|thumb|centre|]] | ||
Правильный тетраэдр можно рассматривать как вырожденный многогранник, однородный двойной дигональный трапецоэдр, содержащий 6 вершин, в двух наборах коллинеарных ребер. | Правильный тетраэдр можно рассматривать как вырожденный многогранник, однородный двойной дигональный трапецоэдр, содержащий 6 вершин, в двух наборах коллинеарных ребер. | ||
[[Файл: | [[Файл:Трапец-07.png|600px|thumb|centre|]] | ||
Процесс усечения, применяемый к тетраэдру, создает ряд однородных многогранников. Усечение ребер до точек дает октаэдр в виде выпрямленного тетраэдра. Процесс завершается как повторное выпрямление, уменьшая исходные грани до точек и снова создавая самодуальный тетраэдр. | Процесс усечения, применяемый к тетраэдру, создает ряд однородных многогранников. Усечение ребер до точек дает октаэдр в виде выпрямленного тетраэдра. Процесс завершается как повторное выпрямление, уменьшая исходные грани до точек и снова создавая самодуальный тетраэдр. | ||
| Строка 323: | Строка 327: | ||
Тетраэдр топологически связан с рядом правильных многогранников и разбиений с вершинами порядка 3. | Тетраэдр топологически связан с рядом правильных многогранников и разбиений с вершинами порядка 3. | ||
[[Файл: | [[Файл:СоедТетр52.png|400px|thumb|right|]] | ||
Интересный многогранник можно построить из пяти пересекающихся тетраэдров. Это соединение из пяти тетраэдров известно уже сотни лет. Он регулярно встречается в мире оригами. Соединение двадцати вершин образует правильный додекаэдр. Существуют как левосторонние, так и правосторонние формы, которые являются зеркальными отражениями друг друга. Наложение обеих форм дает соединение из десяти тетраэдров, в котором десять тетраэдров расположены в виде пяти пар восьмигранных звезд. Восьмигранник стеллы представляет собой соединение двух тетраэдров в двойном положении, и его восемь вершин определяют куб как их выпуклую оболочку. | Интересный многогранник можно построить из пяти пересекающихся тетраэдров. Это соединение из пяти тетраэдров известно уже сотни лет. Он регулярно встречается в мире оригами. Соединение двадцати вершин образует правильный додекаэдр. Существуют как левосторонние, так и правосторонние формы, которые являются зеркальными отражениями друг друга. Наложение обеих форм дает соединение из десяти тетраэдров, в котором десять тетраэдров расположены в виде пяти пар восьмигранных звезд. Восьмигранник стеллы представляет собой соединение двух тетраэдров в двойном положении, и его восемь вершин определяют куб как их выпуклую оболочку. | ||
| Строка 333: | Строка 337: | ||
==Приложения== | ==Приложения== | ||
===Численный анализ=== | ===Численный анализ=== | ||
[[Файл: | [[Файл:Malla irregular de triángulos modelizando una superficie convexa.png|200px|thumb|right|Неправильный объем в пространстве может быть аппроксимирован неправильной триангулированной поверхностью и неправильными элементами тетраэдрического объема.]] | ||
В численном анализе сложные трехмерные формы обычно разбиваются на или аппроксимируются многоугольной сеткой неправильных тетраэдров в процессе составления уравнений для анализа методом конечных элементов, особенно при численном решении уравнений в частных производных. Эти методы имеют широкое практическое применение в вычислительной гидродинамике, аэродинамике, электромагнитных полях, гражданском строительстве, химической инженерии, военно-морской архитектуре и инженерии и смежных областях. | В численном анализе сложные трехмерные формы обычно разбиваются на или аппроксимируются многоугольной сеткой неправильных тетраэдров в процессе составления уравнений для анализа методом конечных элементов, особенно при численном решении уравнений в частных производных. Эти методы имеют широкое практическое применение в вычислительной гидродинамике, аэродинамике, электромагнитных полях, гражданском строительстве, химической инженерии, военно-морской архитектуре и инженерии и смежных областях. | ||
| Строка 348: | Строка 351: | ||
Основная статья: [[Тетраэдрическая молекулярная геометрия]] | Основная статья: [[Тетраэдрическая молекулярная геометрия]] | ||
[[Файл: | [[Файл:Ammonium-3D-balls.png|200px|thumb|left|Ион аммония является тетраэдрическим]] | ||
Форма тетраэдра встречается в природе в ковалентно связанных молекулах. Все sp3-гибридизованные атомы окружены атомами (или одиночными электронными парами) в четырех углах тетраэдра. :Например, в молекуле метана (CH4) или ионааммония (NH+4), четыре атома водорода окружают центральный атом углерода или азота с тетраэдрической симметрией. По этой причине один из ведущих журналов по органической химии называется Tetrahedron. Центральный угол между любыми двумя вершинами идеального тетраэдра равен | Форма тетраэдра встречается в природе в ковалентно связанных молекулах. Все sp3-гибридизованные атомы окружены атомами (или одиночными электронными парами) в четырех углах тетраэдра. :Например, в молекуле метана (CH4) или ионааммония (NH+4), четыре атома водорода окружают центральный атом углерода или азота с тетраэдрической симметрией. По этой причине один из ведущих журналов по органической химии называется Tetrahedron. Центральный угол между любыми двумя вершинами идеального тетраэдра равен | ||
| Строка 362: | Строка 365: | ||
Однако диаграммы четвертичной фазы в технике связи представлены графически на двумерной плоскости. | Однако диаграммы четвертичной фазы в технике связи представлены графически на двумерной плоскости. | ||
[[Файл:Tetrahedral angle calculation.svg|400px|thumb|right| Вычисление центрального угла с помощью скалярного произведения]] | |||
====Электричество и электроника==== | ====Электричество и электроника==== | ||
| Строка 376: | Строка 381: | ||
====Игры==== | ====Игры==== | ||
[[Файл: | [[Файл:4-sided dice 250.jpg|400px|thumb|left|4-сторонний кубик]] | ||
В Царскую игру Ура, датируемую 2600 годом до н.э., играли набором четырехгранных кубиков. | В Царскую игру Ура, датируемую 2600 годом до н.э., играли набором четырехгранных кубиков. | ||
| Строка 390: | Строка 395: | ||
==Тетраэдрический граф== | ==Тетраэдрический граф== | ||
[[Файл: | [[Файл:3-simplex t0 A2.svg|200px|thumb|left|3-кратная симметрия]] | ||
[[Файл: | [[Файл:3-simplex t0.svg|200px|thumb|right|Вершины 4 | ||
Ребра 6 | Ребра 6 | ||
Радиус 1 | Радиус 1 | ||
| Строка 416: | Строка 421: | ||
* [[Трехпрямоугольный тетраэдр]] | * [[Трехпрямоугольный тетраэдр]] | ||
* [[Ортосхема]] | * [[Ортосхема]] | ||
* [[Флогистон]] | |||
* [[Хеддека]] | |||
==Примечания== | ==Примечания== | ||
| Строка 436: | Строка 443: | ||
[[Категория:Дельтаэдры]] | [[Категория:Дельтаэдры]] | ||
[[Категория:Платоновы твердые тела]] | [[Категория:Платоновы твердые тела]] | ||
[[Категория:Отдельные | [[Категория:Отдельные графики]] | ||
[[Категория:Самодуальные многогранники]] | [[Категория:Самодуальные многогранники]] | ||
[[Категория:Призматоидные многогранники]] | [[Категория:Призматоидные многогранники]] | ||
Текущая версия от 19:14, 30 марта 2023
Не путать с тетраэдроидом или тетраэдром (журнал).
В геометрии тетраэдр (множественное число: тетраэдры или тетраэдры), также известный как треугольная пирамида, представляет собой многогранник, состоящий из четырех треугольных граней, шести прямых ребер и четырех вершинных углов. Тетраэдр является самым простым из всех обычных выпуклых многогранников.
Тетраэдр является трехмерным случаем более общей концепции евклидова симплекса, и поэтому его также можно назвать 3-симплексом.
Тетраэдр - это один из видов пирамиды, представляющий собой многогранник с плоским многоугольным основанием и треугольными гранями, соединяющими основание с общей точкой. В случае тетраэдра основанием является треугольник (основанием может считаться любая из четырех граней), поэтому тетраэдр также известен как "треугольная пирамида".
Как и все выпуклые многогранники, тетраэдр можно сложить из одного листа бумаги. Он имеет две такие сетки.
Для любого тетраэдра существует сфера (называемая окружностью), на которой лежат все четыре вершины, и другая сфера (внутренняя сфера), касательная к граням тетраэдра.
Тетраэдр - энергия огня.


Правильный тетраэдр[править]
Правильный тетраэдр - это тетраэдр, все четыре грани которого являются равносторонними треугольниками. Это одно из пяти правильных платоновых тел, которые были известны с древности.
В правильном тетраэдре все грани имеют одинаковый размер и форму (совпадают), а все ребра имеют одинаковую длину.
Правильные тетраэдры сами по себе не образуют мозаики (заполняют пространство), но если их чередовать с правильными октаэдрами в соотношении двух тетраэдров к одному октаэдру, они образуют чередующиеся кубические соты, которые являются тесселяцией. Некоторые тетраэдры, которые не являются правильными, включая ортосхему Шлефли и тетраэдр Хилла, могут складываться в мозаику.
Правильный тетраэдр самодуальен, что означает, что его двойственный является другим правильным тетраэдром. Составная фигура, состоящая из двух таких двойных тетраэдров, образует звездчатый октаэдр или восьмеричный треугольник.
Координаты правильного тетраэдра[править]
Следующие декартовы координаты определяют четыре вершины тетраэдра с длиной ребра 2, центрированные в начале координат, и двумя ровными ребрами:
\left(\pm 1,0,-{\frac {1}{\sqrt {2}}}\right)\quad {\mbox{and}}\quad \left(0,\pm 1,{\frac {1}{\sqrt {2}}}\right)}{ \left(\pm 1,0, -{\frac {1}{\sqrt {2}}}\right)\quad }\справа)}
Выраженный симметрично как 4 точки на единичной сфере, центроид в начале координат, с нижним уровнем грани, вершины:
v_{1}=\left({\sqrt {\frac {8}{9}}},0,-{\frac {1}{3}}\right)}Шаблон:9},0,-{\ фракция {1}{3}}\справа)}
с ребром длиной {\sqrt {\frac {8}{3}}}}{\displaystyle {\sqrt {\frac {8}{3}}}}.
Еще один набор координат основан на чередующемся кубе или полукубе с длиной ребра 2. Эта форма имеет диаграмму Кокстера Узел CDel h.pngCDel 4.pngУзел CDel.pngCDel 3.pngУзел CDel.png и символ Шлефли h{4,3}. Тетраэдр в этом случае имеет длину ребра 2√2. Инвертирование этих координат порождает двойной тетраэдр, а пара вместе образует звездчатый октаэдр, вершины которого являются вершинами исходного куба.
Тетраэдр: (1,1,1), (1,-1,-1), (-1,1,-1), (-1,-1,1)
- Двойной тетраэдр: (-1,-1,-1), (-1,1,1), (1,-1,1), (1,1,-1)
Regular tetrahedron ABCD and its circumscribed sphere
Углы и расстояния[править]
Для правильного тетраэдра с длиной ребра a:

Относительно плоскости основания наклон грани (2√2) в два раза больше, чем у ребра (√2), что соответствует тому факту, что расстояние по горизонтали, пройденное от основания до вершины вдоль ребра, в два раза больше, чем вдоль медианы грани. Другими словами, если C является центроидом основания, расстояние от C до вершины основания в два раза больше, чем от C до середины ребра основания. Это следует из того факта, что медианы треугольника пересекаются в его центре тяжести, и эта точка делит каждый из них на два сегмента, один из которых в два раза длиннее другого (см. Доказательство).
Для правильного тетраэдра с длиной стороны a, радиусом R описывающей его сферы и расстояниями di от произвольной точки в 3-пространстве до его четырех вершин, мы имеем[6]

Изометрии правильного тетраэдра[править]

Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр (см. Выше, а также анимацию, показывающую один из двух тетраэдров в кубе). Симметрии правильного тетраэдра соответствуют половине симметрий куба: те, которые сопоставляют тетраэдры самим себе, а не друг другу.
Тетраэдр является единственным платоновым телом, которое не отображается само на себя путем точечной инверсии.
Правильный тетраэдр имеет 24 изометрии, образуя группу симметрии td, [3,3], (*332), изоморфны симметричной группе, S 4. Их можно классифицировать следующим образом:
T, [3,3]+, (332) изоморфно чередующейся группе, A 4 (тождество и 11 собственных вращений) со следующими классами сопряженности (в скобках указаны перестановки вершин или, соответственно, граней и представление единичного кватерниона):
- идентичность (идентичность; 1)
- вращение вокруг оси через вершину, перпендикулярную противоположной плоскости, на угол ±120°: 4 оси, по 2 на ось, вместе 8 ((1 2 3) и т.д.;
2/1 ± i ± j ± k )
поворот на угол 180° так, чтобы ребро отображалось на противоположное ребро: 3 ((1 2)(3 4), и т.д.; i, j, k)
- отражения в плоскости, перпендикулярной ребру: 6
- отражения в плоскости в сочетании с поворотом на 90 ° вокруг оси, перпендикулярной плоскости: 3 оси, по 2 на ось, вместе 6; эквивалентно, это повороты на 90 ° в сочетании с инверсией (x :отображается на −x): повороты соответствуют поворотам куба относительно лицевой стороныоси
Ортогональные проекции правильного тетраэдра[править]
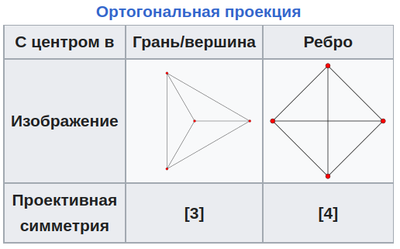
Правильный тетраэдр имеет две специальные ортогональные проекции, одна из которых центрирована на вершине или, что эквивалентно, на грани, а другая центрирована на ребре. Первый соответствует плоскости Кокстера А2
Поперечное сечение правильного тетраэдра[править]


Два косо перпендикулярных противоположных ребра правильного тетраэдра определяют набор параллельных плоскостей. Когда одна из этих плоскостей пересекает тетраэдр, результирующее поперечное сечение представляет собой прямоугольник.[7] Когда пересекающаяся плоскость находится вблизи одного из ребер, прямоугольник длинный и узкий. На полпути между двумя ребрами пересечение представляет собой квадрат. Соотношение сторон прямоугольника меняется на противоположное, когда вы проходите эту промежуточную точку. Для пересечения средней точки квадрата результирующая граничная линия пересекает каждую грань тетраэдра аналогичным образом. Если тетраэдр разделить пополам в этой плоскости, обе половины станут клиньями.
Это свойство также применимо к тетрагональным дисфеноидам при применении к двум специальным парам ребер.
Сферическая черепица[править]
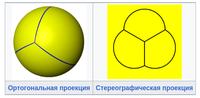
Тетраэдр также может быть представлен в виде сферической плитки и спроецирован на плоскость с помощью стереографической проекции. Эта проекция является конформной, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружности.
Спиральная укладка[править]

Правильные тетраэдры могут быть сложены лицом к лицу в киральную апериодическую цепь, называемую спиралью Бурдейка–Кокстера.
В четырех измерениях все выпуклые правильные 4-многогранники с тетраэдрическими ячейками (5-ячеечные, 16-ячеечные и 600-ячеечные) могут быть построены как разбиения 3-сферы этими цепочками, которые становятся периодическими в трехмерном пространстве граничной поверхности 4-многогранника.
Неправильные тетраэдры[править]


Тетраэдры, у которых нет четырех равносторонних граней, классифицируются и называются по симметриям, которыми они обладают.
Если все три пары противоположных ребер тетраэдра перпендикулярны, то он называется ортоцентрическим тетраэдром. Когда только одна пара противоположных ребер перпендикулярна, это называется полуортоцентрическим тетраэдром.
Изодинамический тетраэдр - это тот, в котором cevians, соединяющие вершины с центрами противоположных граней, совпадают.
Изогонический тетраэдр имеет параллельные cevians, которые соединяют вершины с точками соприкосновения противоположных граней с вписанной сферой тетраэдра.
Трехпрямоугольный тетраэдр[править]
Основная статья: Трехугольный тетраэдр

В трехпрямоугольном тетраэдре три граневых угла в одной вершине являются прямыми углами, как в углу куба.
Кеплер обнаружил связь между кубом, правильным тетраэдром и трехпрямоугольным тетраэдром.
Дисфеноид[править]
Основная статья: Дисфеноид

Дисфеноид - это тетраэдр с четырьмя соответствующими треугольниками в качестве граней; треугольники обязательно имеют все острые углы. Правильный тетраэдр является частным случаем дисфеноида. Другие названия той же формы включают бисфеноид, равнобедренный тетраэдр и равнобедренный тетраэдр.
Ортосхемы[править]

3-ортосхема - это тетраэдр, все четыре грани которого являются прямоугольными треугольниками.[a] Ортосхема - это неправильный симплекс, представляющий собой выпуклую оболочку дерева, в котором все ребра взаимно перпендикулярны. В трехмерной ортосхеме дерево состоит из трех перпендикулярных ребер, соединяющих все четыре вершины линейным путем, который делает два прямоугольных поворота. 3-ортосхема - это тетраэдр, имеющий два прямых угла в каждой из двух вершин, поэтому другое его название - двупрямой тетраэдр. Его также называют четырехугольным тетраэдром, потому что он содержит четыре прямых угла.
Коксетер также называет четырехугольные тетраэдры характерными тетраэдрами из-за их интегральной связи с правильными многогранниками и их группами симметрии.[10] Например, частный случай 3-ортосхемы с перпендикулярными ребрами равной длины характерен для куба, что означает, что куб может быть разделен на экземпляры этой ортосхемы. Если его три перпендикулярных ребра имеют единичную длину, его остальные ребра равны двум длинам √ 2 и одному длине √ 3, поэтому все его ребра являются ребрами или диагоналями куба. КубУзел CDel 1.pngCDel 4.pngУзел CDel.pngCDel 3.pngУзел CDel.png может быть разделен на шесть таких 3-ортосхем Узел CDel.pngCDel 4.pngУзел CDel.pngCDel 3.pngУзел CDel.pngчетырьмя различными способами, причем все шесть окружают одну и ту же диагональ куба √ 3. Куб также может быть разделен на 48 меньших экземпляров этой же характеристической 3-ортосхемы (только одним способом, по всем его плоскостям симметрии сразу).[b] Характерный тетраэдр куба является примером тетраэдра Герона.
Каждый правильный многогранник, включая правильный тетраэдр, имеет свою характерную ортосхему.[c] Существует 3-ортосхема, которая является характеристическим тетраэдром правильного тетраэдра. Правильный тетраэдр Узел CDel 1.pngCDel 3.pngУзел CDel.pngCDel 3.pngУзел CDel.pngподразделяется на 24 экземпляра своего характерного тетраэдра Узел CDel.pngCDel 3.pngУзел CDel.pngCDel 3.pngУзел CDel.pngпо плоскостям симметрии

Если правильный тетраэдр имеет длину ребра 𝒍 = 2, то шесть ребер его характеристического тетраэдра имеют длины {\sqrt {\tfrac {4}{3}}}}{\sqrt {\tfrac {4}{3}}}}, 1}1,{\sqrt {\tfrac {1}{3}}}}{\sqrt {\tfrac {1}{3}}}}(внешняя грань прямоугольного треугольника, характеристический треугольник 𝟀, 𝝓, 𝟁), плюс {\sqrt {\tfrac {3}{2}}}}{\sqrt {\tfrac {3}{2}}}}, {\sqrt {\tfrac {1}{2}}}} {\sqrt {\tfrac {1}{2}}}}, {\sqrt {\tfrac {1}{6}}}}{\sqrt {\tfrac {1}{6}}}}(ребра, являющиеся характерными радиусами правильного тетраэдра). Траектория с тремя ребрами вдоль ортогональных ребер ортосхемы {\displaystyle 1}1, {\sqrt {\tfrac {1}{3}}}}{\sqrt {\tfrac {1}{3}}}}, {\sqrt {\tfrac {1}{6}}}} {\sqrt {\tfrac {1}{6}}}}, сначала от вершины тетраэдра к центру ребра тетраэдра, затем поворачивается на 90 ° к центру грани тетраэдра, затем поворачивается на 90 ° к центру тетраэдра. Ортосхема имеет четыре разные грани прямоугольного треугольника. Внешняя грань представляет собойТреугольник 60-90-30, составляющий одну шестую грани тетраэдра. Тремя внутренними гранями тетраэдра являются: прямоугольный треугольник с ребрами 1}1, {\sqrt {\tfrac {3}{2}}}}{{\sqrt {\tfrac {3}{2}}}}, {\sqrt {\tfrac {1}{2}}}} {\sqrt {\tfrac {1}{2}}}}, прямоугольный треугольник с ребрами {\sqrt {\tfrac {1}{3}}}}{\sqrt {\tfrac {1}{3}}}}, {\sqrt {\tfrac {1}{2}}}} {\sqrt {\tfrac {1}{2}}}}, {\sqrt {\tfrac {1}{6}}}} {\sqrt {\tfrac {1}{6}}}}, и прямоугольный треугольник с ребрами { {\sqrt {\tfrac {4}{3}}}} {\sqrt {\tfrac {4}{3}}}}, {\sqrt {\tfrac {3}{2}}}} {\sqrt {\tfrac {3}{2}}}}, { {\sqrt {\tfrac {1}{6}}}}{{\sqrt {\tfrac {1}{6}}}}.
Тетраэдры, заполняющие пробелы[править]
Тетраэдр, заполняющий пространство, заполняется непосредственно конгруэнтными или энантиоморфными (зеркальными отражениями) копиями самого себя в пространстве плиток.[14] Куб можно разделить на шесть 3-ортосхем, три левосторонних и три правосторонних (по одной на каждой грани куба), и кубы могут заполнять пространство, поэтому характерная 3-ортосхема куба в этом смысле является тетраэдром, заполняющим пространство.[e] Дисфеноид может быть заполняющим пространство тетраэдром в прямом конгруэнтном смысле, как в дисфеноидных тетраэдрических сотах. Однако правильные тетраэдры сами по себе не могут заполнять пространство.[f]
Фундаментальные области[править]

Неправильный тетраэдр, который является фундаментальной областью группы симметрии, является примером тетраэдра Гурса. Тетраэдры Гурса порождают все правильные многогранники (и многие другие однородные многогранники) путем зеркального отражения, процесс, называемый калейдоскопическим построением Витхоффа.
Для многогранников конструкция Вайтоффа располагает три зеркала под углом друг к другу, как в калейдоскопе. В отличие от цилиндрического калейдоскопа, зеркала Витхоффа расположены на трех гранях тетраэдра Гурса таким образом, что все три зеркала пересекаются в одной точке.[g]
Среди тетраэдров Гурса, которые создают трехмерные соты, мы можем распознать ортосхему (характерный тетраэдр куба), двойную ортосхему (характерный тетраэдр куба, связанный с его зеркальным отображением) и заполняющий пространство дисфеноид, показанный выше.[10]Дисфеноид - это двойная ортосхема, связанная гранью со своим зеркальным отражением (четырехугольная ортосхема). Таким образом, все три из этих тетраэдров Гурса и все многогранники, которые они генерируют отражениями, могут быть разделены на характерные тетраэдры куба.
Изометрии неправильных тетраэдров[править]
Изометрии неправильного (немаркированного) тетраэдра зависят от геометрии тетраэдра, возможны 7 случаев. В каждом случае формируется трехмерная точечная группа. Две другие изометрии (C3, [3]+) и (S 4, [2+,4+]) может существовать, если включена маркировка граней или кромок. Тетраэдрические диаграммы включены для каждого типа ниже, с краями, окрашенными по изометрической эквивалентности, и серым цветом для уникальных ребер.
Общие свойства[править]
Объем[править]
Объем тетраэдра определяется формулой объема пирамиды:
V={\frac {1}{3}}A_{0}\,h\,}{\displaystyle V={\frac {1}{3}}A_{0}\,h\,}
где A0 - площадь основания, а h - высота от основания до вершины. Это относится к каждому из четырех вариантов основания, поэтому расстояния от вершин до противоположных граней обратно пропорциональны площадям этих граней.
Для тетраэдра с вершинами a = (a1, a2, a3), b = (b1, b2, b3), c = (c1, c2, c3) и d = (d1, d2, d3) объемявляется 6/1 |det(a − d, b − d, c − d)|, или любая другая комбинация пар вершин, образующих односвязный граф. Это можно переписать, используя скалярное произведение и перекрестное произведение, что дает
V={\frac {|(\mathbf {a} -\mathbf {d} )\cdot ((\mathbf {b} -\mathbf {d} )\times (\mathbf {c} -\mathbf {d} ))|}{6}}.}V={\frac {|(\mathbf {a} -\mathbf {d} )\cdot ((\mathbf {b} -\mathbf {d} )\times (\mathbf {c} -\mathbf {d} ))|}{6}}.
Если начало координат выбрано так, чтобы оно совпадало с вершиной d, то d = 0, поэтому
V={\frac {|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}{6}},}V={\frac {|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}{6}},
где a, b и c представляют три ребра, которые встречаются в одной вершине, а a · (b × c) - скалярное тройное произведение. Сравнивая эту формулу с формулой, используемой для вычисления объема параллелепипеда, мы приходим к выводу, что объем тетраэдра равен 6/1
объема любого параллелепипеда, у которого есть три сходящихся ребра.
Абсолютное значение скалярного тройного произведения может быть представлено в виде следующих абсолютных значений определителей:
где индексы i, j ∈ {1, 2, 3, 4} представляют вершины {a, b, c, d}, а d ij – попарное расстояние между ними, т.е. Длина ребра, соединяющего две вершины. Отрицательное значение определителя означает, что тетраэдр не может быть построен с заданными расстояниями. Эта формула, иногда называемая формулой Тартальи, по сути, принадлежит художнику Пьеро делла Франческа в 15 веке, как трехмерный аналог формулы Герона 1-го века для площади треугольника.
Пусть a, b, c - три ребра, которые встречаются в точке, а x, y, z - противоположные ребра. Пусть V - объем тетраэдра; тогда
В приведенной выше формуле используется шесть длин ребер, а в следующей формуле используются три длины ребер и три угла.
Формула типа Герона для объема тетраэдра[править]

Если U, V, W, u, v, w - длины ребер тетраэдра (первые три образуют треугольник; с u напротив U, v напротив V, w напротив W), то[
Делитель объема[править]
Любая плоскость, содержащая бимедиан (соединитель середин противоположных ребер) тетраэдра, делит объем тетраэдра пополам.[19]
Неевклидов объем[править]
Для тетраэдров в гиперболическом пространстве или в трехмерной эллиптической геометрии двугранные углы тетраэдра определяют его форму и, следовательно, его объем. В этих случаях объем задается формулой Мураками–Яно.[20] Однако в евклидовом пространстве масштабирование тетраэдра изменяет его объем, но не двугранные углы, поэтому такой формулы существовать не может.
Расстояние между ребрами[править]
Любые два противоположных ребра тетраэдра лежат на двух косых линиях, а расстояние между ребрами определяется как расстояние между двумя косыми линиями. Пусть d − расстояние между косыми линиями, образованными противоположными ребрами a и b - c, как рассчитано здесь. Тогда другая формула объема задается
V={\frac {d|(\mathbf {a} \times \mathbf {(b-c)} )|}{6}}.}V={\frac {d|(\mathbf {a} \times \mathbf {(b-c)} )|}{6}}.
Свойства, аналогичные свойствам треугольника[править]
Тетраэдр обладает многими свойствами, аналогичными свойствам треугольника, включая внутреннюю сферу, окружность, средний тетраэдр и внешние сферы. Он имеет соответствующие центры, такие как incenter, circumcenter, excenters, центр Спайкера и точки, такие как центроид. Однако, как правило, нет ортоцентра в смысле пересекающихся высот.
Гаспар Монж нашел центр, который существует в каждом тетраэдре, теперь известный как точка Монжа: точка, в которой пересекаются шесть средних плоскостей тетраэдра. Средняя плоскость определяется как плоскость, ортогональная ребру, соединяющему любые две вершины, которая также содержит центр тяжести противоположного ребра, образованного путем соединения двух других вершин. Если высоты тетраэдра пересекаются, то точка Монжа и ортоцентр совпадают, что дает класс ортоцентрического тетраэдра.
Ортогональная прямая, проведенная от точки Монжа к любой грани, пересекается с этой гранью в средней точке отрезка прямой между ортоцентром этой грани и основанием высоты, перенесенной из противоположной вершины.
Отрезок прямой, соединяющий вершину тетраэдра с центром тяжести противоположной грани, называется медианой, а отрезок прямой, соединяющий середины двух противоположных ребер, называется бимедианом тетраэдра. Следовательно, в тетраэдре четыре медианы и три бимедианы. Все эти семь отрезков параллельны в точке, называемой центроидом тетраэдра. Кроме того, четыре медианы делятся центроидом в соотношении 3:1 (см. теорему Коммандино). Центроид тетраэдра - это средняя точка между его точкой Монжа и центром окружности. Эти точки определяютЛиния Эйлера тетраэдра, аналогичная линии Эйлера треугольника.
Девятиконечная окружность общего треугольника имеет аналог в окружности медиального тетраэдра тетраэдра. Это двенадцатиконечная сфера, и, помимо центроидов четырех граней эталонного тетраэдра, она проходит через четыре замещающие точки Эйлера, одну треть пути от точки Монжа к каждой из четырех вершин. Наконец, он проходит через четыре базовые точки ортогональных прямых, отброшенных от каждой точки Эйлера к грани, не содержащей вершины, которая породила точку Эйлера.
Центр T двенадцатиконечной сферы также лежит на прямой Эйлера. В отличие от своего треугольного аналога, этот центр лежит на одной трети пути от точки Монжа M к центру окружности. Кроме того, ортогональная прямая через T к выбранной грани является компланарной с двумя другими ортогональными прямыми к той же грани. Первая представляет собой ортогональную прямую, проходящую через соответствующую точку Эйлера к выбранной грани. Вторая представляет собой ортогональную прямую, проходящую через центр тяжести выбранной грани. Эта ортогональная прямая, проходящая через двенадцатиточечный центр, лежит на полпути между ортогональной прямой Эйлера и ортогональной центроидной линией. Кроме того, для любой грани центр с двенадцатью точками находится в средней точке соответствующей точки Эйлера и ортоцентра для этой грани.
Радиус двенадцатиконечной сферы составляет одну треть радиуса окружности эталонного тетраэдра.
Существует связь между углами, образованными гранями общего тетраэдра, заданными
где α ij - угол между гранями i и j.
Геометрическая медиана координат положения вершины тетраэдра и его изогонического центра связаны при обстоятельствах, аналогичных наблюдаемым для треугольника. Лоренц Линделеф обнаружил, что любому данному тетраэдру соответствует точка, известная сейчас как изогонический центр, O, в которой телесные углы, уменьшенные гранями, равны, имеют общее значение π sr, и в которой углы, уменьшенные противоположными ребрами, равны.[25] Телесный угол π sr составляет одну четверть от того, что вычитается из всего пространства. Когда все телесные углы в вершинах тетраэдра меньше π sr, O лежит внутри тетраэдра, и поскольку сумма расстояний от O до вершин минимальна, O совпадает с геометрической медианой M вершин. В случае, если телесный угол в одной из вершин, v, измеряет в точности π sr, то O и M совпадают с v. Однако, если тетраэдр имеет вершину, v, с телесным углом больше, чем π sr, M все равно соответствует v, но O лежит за пределами тетраэдра.
Геометрические соотношения[править]
Тетраэдр является 3-симплексным. В отличие от случая других платоновых тел, все вершины правильного тетраэдра равноудалены друг от друга (это единственно возможное расположение четырех равноудаленных точек в трехмерном пространстве).
Тетраэдр представляет собой треугольную пирамиду, а правильный тетраэдр самодуальен.
Правильный тетраэдр может быть встроен в куб двумя способами, так что каждая вершина является вершиной куба, а каждое ребро является диагональю одной из граней куба. Для одного такого вложения декартовы координаты вершин равны
(+1, +1, +1);
- (−1, −1, +1);
- (−1, +1, −1);
- (+1, −1, −1).
- Это дает тетраэдр с длиной ребра 2√ 2, центрированный в начале координат. Для другого тетраэдра (который двойствен первому) переверните все знаки. Объединенные вершины этих двух тетраэдров являются вершинами куба, демонстрируя, что правильный тетраэдр является 3-полукубом.
Объем этого тетраэдра составляет одну треть объема куба. Объединение обоих тетраэдров дает правильное многогранное соединение, называемое соединением двух тетраэдров или восьмеричной стеллой.
Внутренняя часть восьмерика стеллы представляет собой октаэдр, и, соответственно, правильный октаэдр является результатом отрезания от правильного тетраэдра четырех правильных тетраэдров вдвое меньшего линейного размера (т.е. выпрямления тетраэдра).
Приведенное выше вложение делит куб на пять тетраэдров, один из которых правильный. Фактически, пять - это минимальное количество тетраэдров, необходимое для составления куба. Чтобы увидеть это, начиная с базового тетраэдра с 4 вершинами, каждый добавленный тетраэдр добавляет не более 1 новой вершины, поэтому необходимо добавить еще как минимум 4, чтобы получился куб с 8 вершинами.
Вписывание тетраэдров внутрь правильного соединения из пяти кубов дает еще два правильных соединения, содержащих пять и десять тетраэдров.
Правильные тетраэдры сами по себе не могут мозаизировать пространство, хотя этот результат кажется достаточно вероятным, чтобы Аристотель утверждал, что это возможно. Однако два правильных тетраэдра могут быть объединены с октаэдром, давая ромбоэдр, который может перекрывать пространство в виде четырехгранно-октаэдрических сот.
Однако известно несколько неправильных тетраэдров, копии которых могут покрывать пространство, например, характерная ортосхема куба и дисфеноид дисфеноидных тетраэдрических сот. Полный список остается открытой проблемой.
Если ослабить требование, чтобы все тетраэдры были одинаковой формы, можно разбить пространство на плитки, используя только тетраэдры многими различными способами. Например, можно разделить октаэдр на четыре одинаковых тетраэдра и снова объединить их с двумя правильными. (В качестве дополнительного примечания: эти два вида тетраэдров имеют одинаковый объем.)
Тетраэдр уникален среди однородных многогранников тем, что не имеет параллельных граней.
Закон синусов для тетраэдров и пространство всех форм тетраэдров[править]
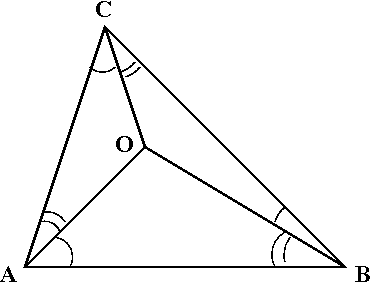
Следствием обычного закона синусов является то, что в тетраэдре с вершинами O, A, B, C мы имеем
\sin \angle OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.\,}\sin \ угол OAB \ cdot \ sin \ угол OBC \ cdot \ sin \ угол OCA = \sin \ угол OAC \ cdot \ sin \ угол OCB \ cdot \ sin \ угол OBA.\,
- Можно рассматривать две стороны этого тождества как соответствующие ориентации поверхности по часовой стрелке и против часовой стрелки.
Помещение любой из четырех вершин в роль O дает четыре таких тождества, но не более трех из них являются независимыми: если стороны "по часовой стрелке" трех из них умножаются и произведение выводится равным произведению сторон "против часовой стрелки" тех же трех тождеств,и тогда общие факторы отменяются с обеих сторон, результатом является четвертое тождество.
Три угла являются углами некоторого треугольника тогда и только тогда, когда их сумма равна 180 ° (π радиан). Какое условие для 12 углов необходимо и достаточно для того, чтобы они были 12 углами некоторого тетраэдра? Очевидно, что сумма углов любой стороны тетраэдра должна составлять 180 °. Поскольку существует четыре таких треугольника, существует четыре таких ограничения на суммы углов, и число степеней свободы, таким образом, уменьшается с 12 до 8. Четыре соотношения, заданные этим законом синуса, еще больше уменьшают число степеней свободы, с 8 до не 4, а 5, поскольку четвертое ограничение не является независимым от первых трех. Таким образом, пространство всех форм тетраэдров является 5-мерным.[27]
Закон косинусов для тетраэдров[править]
Основная статья: Тригонометрия тетраэдра
Пусть {P1, P2, P3, P4} - точки тетраэдра. Пусть δi - площадь грани, противоположной вершине pi, и пусть θ ij - двугранный угол между двумя гранями тетраэдра, смежными с ребром Pi pj.
Закон косинусов для этого тетраэдра,[28] который связывает площади граней тетраэдра с двугранными углами вокруг вершины, задается следующим соотношением:
\Delta _{i}^{2}=\Delta _{j}^{2}+\Delta _{k}^{2}+\Delta _{l}^{2}-2(\Delta _{ik}+\Delta _{k}\Delta _{l}\cos \theta _{ij})}\cos \тета _{ij})
Внутренняя точка[править]
Пусть P - любая внутренняя точка тетраэдра объема V, вершинами которого являются A, B, C и D, и для которого площади противоположных граней равны fa, fb, fc и fd. Затем[29]: стр.62, #1609
PA\cdot F_{\mathrm {a} }+PB\cdot F_{\mathrm {b} }+PC\cdot F_{\mathrm {c} }+PD\cdot F_{\mathrm {d} }\geq 9V.}{\displaystyle PA\cdot F_{\mathrm {a} }+PB\cdot F_{\mathrm {b}}+PC\cdot F_{\mathrm {c}}+PD\cdot F_{\mathrm {d} }\geq 9V.}
- Для вершин A, B, C и D, внутренней точки P и футов J, K, L и M перпендикуляров от P к граням, и предположим, что грани имеют равные площади, тогда[29]: стр.226, # 215
PA+PB+PC+PD\geq 3(PJ+PK+PL+PM).}PA+PB+ PC+PD\geq 3(PJ + PK+ PL + PM).
В излучении[править]
Обозначая радиус тетраэдра как r, а радиусы его треугольных граней как r i для i = 1, 2, 3, 4, мы имеем[29]: стр.81, #1990
{\frac {1}{r_{1}^{2}}}+{\frac {1}{r_{2}^{2}}}+{\frrac {r^{2}}},}{\frac {1}{r_{1}^{2}}}+{\ фракция {1}{r_{2}^{2}}}+{\ фракция {1}{r_{3}^{2}}}+{\ фракция {1}{r_{4r^{2}}},
с равенством тогда и только тогда, когда тетраэдр правильный.
Если A 1, A 2, A 3 и A 4 обозначают площадь каждой грани, значение r определяется как
r={\frac {3V}{A_{1}+A_{2}+A_{3}+A_{4}}}}{\displaystyle r={\frac {3V}{A_{1}+A_{2}+A_{3}+A_{4}}}}.
Эта формула получается путем деления тетраэдра на четыре тетраэдра, точки которых являются тремя точками одной из исходных граней и центром. Поскольку четыре субтетраэдра заполняют объем, мы имеем V={\frac {1}{3}}A_{1}r+{\frac {1}{3}}A_{2}r+{\frac {1}{3}}A_{3}r+{\frac {1}{3}}A_{4}r}{\displaystyle V={\frac {1}{3}}A_{1}r+{\frac {1}{3}}A_{2}r+{\frac {1}{3}}A_{3}r+{\frac {1}{3}}A_{4}r}.
Радиус окружности[править]
Обозначим радиус окружности тетраэдра как R. Пусть a, b, c - длины трех ребер, которые встречаются в вершине, а A, B, C - длины противоположных ребер. Пусть V - объем тетраэдра. Затем
R={\frac {\sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.}{\displaystyle R={\frac {\sqrt {(aA+bB+cC)(aA+bB-cC)(aA-bB+cC)(-aA+bB+cC)}}{24V}}.}
Центр окружности[править]
Центр окружности тетраэдра можно найти как пересечение трех биссектрис. Плоскость биссектрисы определяется как плоскость, центрированная на и ортогональная ребру тетраэдра. С помощью этого определения центр окружности C тетраэдра с вершинами x0, x1, x2, x3 может быть сформулирован как матрично-векторное произведение:[32]
{n{выровненный}C&=A^{-1}B&{\text{где}}&\ &A=\left({\beg{T}\\\слева[x_{2\|^{2 }-x_{0} \справа]^{T}\\\слева[x_{3}-x_{0}\справа]^{T}\конец{матрицы}}\справа) &\ &{\те({\begin{кстматрица}\^{2}\ конец{матрица}}\справа)\\\конец{выровненный}}}
- В отличие от центроида, центр окружности не всегда может находиться внутри тетраэдра. Аналогично тупому треугольнику, центр окружности тупого тетраэдра находится за пределами объекта.
Центроид[править]
Центр масс тетраэдра вычисляется как среднее арифметическое его четырех вершин, см. Центроид.
Грани[править]
Сумма площадей любых трех граней больше площади четвертой грани..225, #159
Целочисленные тетраэдры[править]
Основная статья: Тетраэдр Герона Существуют тетраэдры, имеющие целочисленные длины ребер, площади граней и объем. Они называются тетраэдрами Герона. Один пример имеет одно ребро 896, противоположное ребро 990 и остальные четыре ребра 1073; две грани представляют собой равнобедренные треугольники площадью 436 800, а две другие равнобедренные треугольники площадью 47 120, а объем равен 124 185 600.
Тетраэдр может иметь целочисленный объем и последовательные целые числа в качестве ребер, примером может служить тетраэдр с ребрами 6, 7, 8, 9, 10, и 11, и том 48.
Связанные многогранники и соединения[править]

Правильный тетраэдр можно рассматривать как вырожденный многогранник, однородную дигональную антипризму, где базовые многоугольники являются редуцированными дигонами.

Правильный тетраэдр можно рассматривать как вырожденный многогранник, однородный двойной дигональный трапецоэдр, содержащий 6 вершин, в двух наборах коллинеарных ребер.
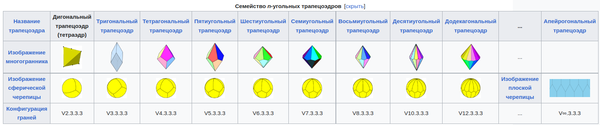
Процесс усечения, применяемый к тетраэдру, создает ряд однородных многогранников. Усечение ребер до точек дает октаэдр в виде выпрямленного тетраэдра. Процесс завершается как повторное выпрямление, уменьшая исходные грани до точек и снова создавая самодуальный тетраэдр.
Семейство однородных четырехгранных многогранников
Этот многогранник топологически связан как часть последовательности правильных многогранников с символами Шлефли {3,n}, продолжающимися в гиперболической плоскости.
Тетраэдр топологически связан с рядом правильных многогранников и разбиений с вершинами порядка 3.

Интересный многогранник можно построить из пяти пересекающихся тетраэдров. Это соединение из пяти тетраэдров известно уже сотни лет. Он регулярно встречается в мире оригами. Соединение двадцати вершин образует правильный додекаэдр. Существуют как левосторонние, так и правосторонние формы, которые являются зеркальными отражениями друг друга. Наложение обеих форм дает соединение из десяти тетраэдров, в котором десять тетраэдров расположены в виде пяти пар восьмигранных звезд. Восьмигранник стеллы представляет собой соединение двух тетраэдров в двойном положении, и его восемь вершин определяют куб как их выпуклую оболочку.
Квадратный хосоэдр - это еще один многогранник с четырьмя гранями, но у него нет треугольных граней.
Многогранник Силаси и тетраэдр - единственные два известных многогранника, у которых каждая грань имеет ребро друг с другом. Кроме того, многогранник Часара (сам по себе является двойственным многограннику Силаси) и тетраэдр являются единственными двумя известными многогранниками, в которых каждая диагональ лежит на сторонах.
Приложения[править]
Численный анализ[править]

В численном анализе сложные трехмерные формы обычно разбиваются на или аппроксимируются многоугольной сеткой неправильных тетраэдров в процессе составления уравнений для анализа методом конечных элементов, особенно при численном решении уравнений в частных производных. Эти методы имеют широкое практическое применение в вычислительной гидродинамике, аэродинамике, электромагнитных полях, гражданском строительстве, химической инженерии, военно-морской архитектуре и инженерии и смежных областях.
Проектирование конструкций[править]
Тетраэдр, имеющий жесткие ребра, по своей природе является жестким. По этой причине его часто используют для придания жесткости каркасным конструкциям, таким как пространственные рамы.
Авиация[править]
На некоторых аэродромах большая рама в форме тетраэдра с двумя сторонами, покрытыми тонким материалом, установлена на вращающейся оси и всегда направлена против ветра. Он построен достаточно большим, чтобы его можно было увидеть с воздуха, и иногда его освещают. Его назначение - служить ориентиром для пилотов, указывающих направление ветра.
Химия[править]
Основная статья: Тетраэдрическая молекулярная геометрия
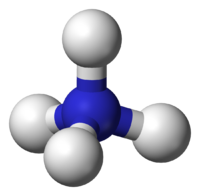
Форма тетраэдра встречается в природе в ковалентно связанных молекулах. Все sp3-гибридизованные атомы окружены атомами (или одиночными электронными парами) в четырех углах тетраэдра. :Например, в молекуле метана (CH4) или ионааммония (NH+4), четыре атома водорода окружают центральный атом углерода или азота с тетраэдрической симметрией. По этой причине один из ведущих журналов по органической химии называется Tetrahedron. Центральный угол между любыми двумя вершинами идеального тетраэдра равен
arccos(− 3/1 ), или приблизительно 109,47°.
Вода, H2o , также имеет тетраэдрическую структуру с двумя атомами водорода и двумя одиночными парами электронов вокруг центральных атомов кислорода. Однако его тетраэдрическая симметрия не идеальна, поскольку одиночные пары отталкивают больше, чем одиночные O–H связи.
Диаграммы четвертичных фаз смесей химических веществ представлены графически в виде тетраэдров.
Однако диаграммы четвертичной фазы в технике связи представлены графически на двумерной плоскости.

Электричество и электроника[править]
Основные статьи: Электричество и электроника
Если шесть равных резисторов спаяны вместе, образуя тетраэдр, то сопротивление, измеренное между любыми двумя вершинами, составляет половину сопротивления одного резистора.[36][37]
Поскольку кремний является наиболее распространенным полупроводником, используемым в твердотельной электронике, а валентность кремния равна четырем, тетраэдрическая форма четырех химических связей в кремнии оказывает сильное влияние на то, как образуются кристаллы кремния и какие формы они принимают.
Цветовое пространство[править]
Основная статья: Цветовое пространство
Тетраэдры используются в алгоритмах преобразования цветового пространства специально для случаев, когда ось яркости диагонально сегментирует цветовое пространство (например, RGB, CMY).[38]
Игры[править]

В Царскую игру Ура, датируемую 2600 годом до н.э., играли набором четырехгранных кубиков.
Особенно в ролевых играх это твердое тело известно как 4-сторонний кубик, один из наиболее распространенных многогранных кубиков, с выпавшим числом, появляющимся вокруг нижней или верхней вершины. Некоторые головоломки, похожие на кубики Рубика, являются четырехгранными, такими как Пираминкс и Пираморфикс.
Геология[править]
Основная статья: Тетраэдрическая гипотеза Тетраэдрическая гипотеза, первоначально опубликованная Уильямом Лоутианом Грином для объяснения образования Земли, была популярна в начале 20-го века.
Популярная культура[править]
По словам Марвина Мински, ученого-когнитивиста и эксперта по искусственному интеллекту, который консультировал Кубрика по поводу компьютера HAL 9000 и других аспектов фильма, Стэнли Кубрик изначально задумывал монолит в 2001: Космическая одиссея в виде тетраэдра. Кубрик отказался от идеи использования тетраэдра, поскольку посетитель, увидевший видеозапись, не узнал, что это такое, и он не хотел, чтобы в фильме было что-то непонятное обычным людям.
Тетраэдрический граф[править]


Скелет тетраэдра (состоящий из вершин и ребер) образует граф с 4 вершинами и 6 ребрами. Это частный случай полного графа, K 4, и кругового графа, W 4.[43]Это один из 5 платоновых графов, каждый из которых представляет собой скелет своего платонова твердого тела.
Смотри также[править]
Спираль Бурдейка–Кокстера * Конфигурация Мебиуса * Калтроп * Полугиперкуб и симплекс - n-мерные аналоги * Пентахорон – 4-мерный аналог * Синергетика (более полная) * Четырехгранный воздушный змей
- Тетраэдрическое число
- Упаковка тетраэдра
- Треугольная дипирамида – построена путем соединения двух тетраэдров вдоль одной грани
- Трехпрямоугольный тетраэдр
- Ортосхема
- Флогистон
- Хеддека
Примечания[править]
- 3-ортосхема не является дисфеноидом, поскольку ее противоположные ребра имеют разную длину. Невозможно построить дисфеноид с гранями прямоугольного треугольника или тупого треугольника.
- Для правильного k-многогранника диаграмма Кокстера-Дынкина характеристической k-ортосхемы представляет собой диаграмму k-многогранника без кольца образующих точек. Правильный k-многогранник подразделяется по своей симметрии (k-1)-элементов на g экземпляров его характеристической k-ортосхемы, которые окружают его центр, где g - порядок группы симметрии k-многогранника.
- Правильный многогранник размерности k имеет характеристическую k-ортосхему, а также характеристическую (k-1)-ортосхему. У правильного многогранника есть характерный тетраэдр (3-ортосхема), на который он подразделяется своими плоскостями симметрии, а также характерный треугольник (2-ортосхема), на который его поверхность подразделяется линиями симметрии его граней. После разделения его поверхности на характерные прямоугольные треугольники, окружающие центр каждой грани, его внутреннюю часть можно разделить на характерные тетраэдры, добавив радиусы, соединяющие вершины прямоугольных треугольников поверхности с центром многогранника.Образованные таким образом внутренние треугольники также будут прямоугольными треугольниками.
- Характерной ортосхемой куба является один из тетраэдров Хилла, семейства тетраэдров, заполняющих пространство. Все тетраэдры, заполняющие пространство, являются ножницами, соответствующими кубу. Каждый выпуклый многогранник ножницеобразно соответствует ортосхеме. Каждый правильный выпуклый многогранник (платоново твердое тело) может быть разбит на некоторое четное число экземпляров его характерной ортосхемы.
- Четырехгранно-октаэдрические соты заполняют пространство чередующимися правильными ячейками тетраэдра и правильными ячейками октаэдра в соотношении 2:1.
- Диаграмма Кокстера-Дынкина сгенерированного многогранника содержит три узла, представляющие три зеркала. На диаграмме закодирован двугранный угол между каждой парой зеркал, а также местоположение единственной образующей точки, которая умножается на зеркальные отражения в вершинах многогранника. Для правильного многогранника диаграмма Кокстера-Дынкина ортосхемы
производящей характеристики представляет собой диаграмму сгенерированного многогранника без маркировки образующей точки.
Библиография[править]
mathworld.wolfram.com/Tetrahedron.html
Пруф[править]
.polyhedra.net/en/model.php?name-en=tetrahedron
[[]]