Аналитическая геометрия
Эта статья посвящена координатной геометрии. Для изучения аналитических многообразий см. раздел Алгебраическая геометрия § аналитическая геометрия .
В классической математике аналитическая геометрия, также известная как координатная геометрия или декартова геометрия , является изучением геометрии с использованием системы координат . Это контрастирует с синтетической геометрией .
Аналитическая геометрия широко используется в физике и технике , а также в авиации , ракетостроении , космической науке и космическом полете . Это основа большинства современных областей геометрии, в том числе алгебраической , дифференциальной , дискретной и вычислительной геометрии .
Обычно Декартовая система координат применяется для управления уравнениями для плоскостей, прямых линий и квадратов , часто в двух, а иногда и в трех измерениях. Геометрически изучается евклидова плоскость ( два измерения ) и евклидово пространство (три измерения ). Как учат в школьных учебниках, аналитическая геометрия может быть объяснена более просто: она связана с определением и представлением геометрических фигур численным способом и извлечением числовой информации из числовых определений и представлений фигур. Что алгебра вещественных чисел может быть использован для получения результатов о линейном континууме геометрии опирается на аксиому Кантора–Дедекинда
История[править]
Древняя Греция[править]
Греческий математик Менехм решал задачи и доказывал теоремы с помощью метода, который имел сильное сходство с использованием координат, и иногда утверждалось, что он ввел аналитическую геометрию.
Аполлоний Пергский в своей книге "о детерминированном сечении" рассматривал проблемы таким образом, что их можно было бы назвать аналитической геометрией одного измерения; с вопросом о нахождении точек на прямой, которые находились бы в отношении к другим.[2] Аполлоний в конических системах развил метод, который настолько похож на аналитическую геометрию, что его работа иногда считается предвосхищением работы Декарта примерно на 1800 лет. Его применение опорных линий, диаметра и касательной существенно не отличается от нашего современного использования системы координат, где расстояния, измеренные вдоль диаметра от точки касания, являются абсциссами, а сегменты, параллельные касательной и перехваченные между осью и кривой, являются ординатами. Он далее развил отношения между абсциссами и соответствующими ординатами, которые эквивалентны риторическим уравнениям кривых. Однако, хотя Аполлоний вплотную подошел к разработке аналитической геометрии, ему это не удалось, так как он не учитывал отрицательные величины и во всех случаях система координат накладывалась на заданную кривую апостериорно, а не априорно . То есть уравнения были определены кривыми, но кривые не были определены уравнениями. Координаты, переменные и уравнения были вспомогательными понятиями, применяемыми к конкретной геометрической ситуации.
Персия[править]
Персидский математик XI века Омар Хайям видел сильную связь между геометрией и алгеброй и двигался в правильном направлении, когда он помог закрыть разрыв между численной и геометрической алгеброй с его геометрическим решением общих кубических уравнений , но решающий шаг пришел позже с Декартом. Омару Хайяму приписывают выявление основ алгебраической геометрии , а также его книжный Трактат о демонстрациях задач алгебры (1070), который заложил принципы алгебры, является частью тела персидской математики, которая в конечном итоге была передана в Европу. благодаря своему основательному геометрическому подходу к алгебраическим уравнениям Хайяма можно считать предшественником Декарта в изобретении аналитической геометрии.
Западная Европа[править]
Аналитическая геометрия была независимо изобретена Рене Декартом и Пьером де Ферма , хотя Декарту иногда уделяется единственное внимание. декартова геометрия , альтернативный термин, используемый для аналитической геометрии, назван в честь Декарта.
Декарт добился значительного прогресса с методами в эссе под названием La Geometrie (геометрия) , одном из трех сопутствующих эссе (приложений), опубликованных в 1637 году вместе с его дискурсом о методе для правильного направления своего разума и поиска истины в науках, обычно называемом дискурсом о методе . Эта работа, написанная на его родном французском языке и ее философские принципы, послужили основой для исчисления в Европе. Первоначально эта работа не была хорошо воспринята, отчасти из-за многочисленных пробелов в аргументации и сложных уравнений. Только после перевода на латынь и добавления комментария Ван Схотена в 1649 году (и дальнейшей работы после этого) шедевр Декарта получил должное признание.
Пьер де Ферма также был пионером в развитии аналитической геометрии. Хотя он и не был опубликован при его жизни, рукописная форма Ad locos planos et solidos isagoge (введение в плоские и твердые локусы) была распространена в Париже в 1637 году, непосредственно перед публикацией дискурса Декарта . четко написано и хорошо принято, введение также заложена основа для аналитической геометрии. Ключевое различие между обработками ферма и Декарта заключается в точке зрения: ферма всегда начинал с алгебраического уравнения, а затем описывал геометрическую кривую, которая его удовлетворяла, тогда как Декарт начинал с геометрических кривых и производил свои уравнения как одно из нескольких свойств кривых. Как следствие этого подхода, Декарту пришлось иметь дело с более сложными уравнениями, и он должен был разработать методы работы с полиномиальными уравнениями более высокой степени. Именно Леонард Эйлер впервые применил координатный метод в систематическом исследовании пространственных кривых и поверхностей.
Координаты[править]
Основная статья: Системы координат
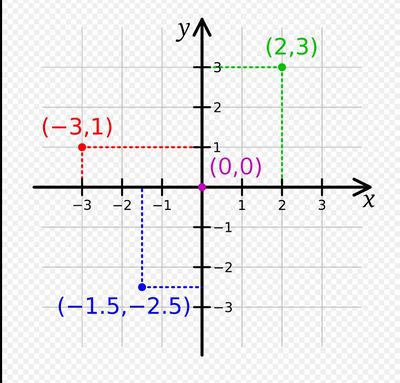
В аналитической геометрии плоскости задается система координат, по которой каждая точка имеет пару действительных числовых координат. Аналогично, Евклидово пространство задается координатами, где каждая точка имеет три координаты. Значение координат зависит от выбора начальной точки начала координат. Существует множество используемых систем координат, но наиболее распространенными являются следующие:
Декартовые координаты (в плоскости или пространстве)[править]
Основная статья: Декартова система координат
Наиболее распространенной системой координат является Декартовая система координат , в которой каждая точка имеет координату x, представляющую ее горизонтальное положение, и координату y, представляющую ее вертикальное положение. Они обычно записываются в виде упорядоченной пары (x, y ). Эта система также может быть использована для трехмерной геометрии , где каждая точка в евклидовом пространстве представлена упорядоченной тройкой координат ( x , y, z ).
Полярные координаты (в плоскости)[править]
Основная статья: Полярные координаты
В полярных координатах каждая точка плоскости представлена своим расстоянием r от начала координат и своим углом θ , причем θ обычно измеряется против часовой стрелки от положительной оси X. Используя эту нотацию, точки обычно записываются в виде упорядоченной пары (r, θ). Можно переходить взад и вперед между двумерными Декартовыми и полярными координатами, используя следующие формулы:
x = r c o s θ , y = r s i n θ ; r = x 2 + y 2 , θ = arctan ( y / x ) }.
Эта система может быть обобщена на трехмерное пространство с помощью использования цилиндрических или сферических координат.
Цилиндрические координаты (в пространстве) Основная статья: цилиндрические координаты
В цилиндрических координатах каждая точка пространства представлена своей высотой z, радиусом r от оси z и углом θ, который образует ее проекция на плоскость xy относительно горизонтальной оси.
Сферические координаты (в пространстве)[править]
Основная статья: Сферические координаты
В сферических координатах каждая точка пространства представлена своим расстоянием ρ от начала координат, углом θ его проекции на плоскость xy относительно горизонтальной оси и углом φ, который он делает относительно оси Z. Названия углов в физике часто меняются местами.
Уравнения и кривые[править]
Основные статьи: Набор решений и Локус (математика)
В аналитической геометрии любое уравнение, связанное с координатами, задает подмножество плоскости, а именно набор решений для уравнения или локус . Например, уравнение y = x соответствует множеству всех точек на плоскости, координаты x и y которых равны. Эти точки образуют линию, и y = x, как говорят, является уравнением для этой линии. В общем случае линейные уравнения, включающие x и y, задают линии , квадратичные уравнения задают конические сечения, а более сложные уравнения описывают более сложные фигуры.
Обычно одно уравнение соответствует кривой на плоскости. Это не всегда так: тривиальное уравнение x = x определяет всю плоскость, а уравнение x 2 + y 2 = 0 определяет только одну точку (0, 0). В трехмерном пространстве одно уравнение обычно дает поверхность, и кривая должна быть определена как пересечение двух поверхностей (см. ниже) или как система параметрических уравнений . уравнение x 2 + y 2 = r 2 является уравнением для любой окружности, центрированной в начале координат (0, 0) с радиусом r.
Линии и плоскости[править]
Основные статьи: Линия (геометрия) и Плоскость (геометрия)
Линии в декартовой плоскости, или в более общем случае , в аффинных координатах, могут быть описаны алгебраически линейными уравнениями. В двух измерениях уравнение для не-вертикальных линий часто задается в форме склон-перехват:
- y = m x + b
где:
- m-наклон или градиент линии.
- b - это y-перехват линии.
- x-независимая переменная функции y = f (x ).
Аналогично тому, как линии в двумерном пространстве описываются с помощью точечно-наклонной формы для их уравнений, плоскости в трехмерном пространстве имеют естественное описание, используя точку на плоскости и вектор, ортогональный ей (нормальный вектор), чтобы указать ее "наклон".
В частности, пусть r 0 }это вектор положения некоторой точки P 0 = ( x 0 , y 0 , z 0 ) ), и пусть n = ( a , b , c )это ненулевой вектор. Плоскость, определяемая этой точкой и вектором, состоит из этих точек P Пс вектором положения r , таким что вектор, проведенный от P 0 }до P П, перпендикулярен n } . Напоминая, что два вектора перпендикулярны тогда и только тогда, когда их точечное произведение равно нулю, следует, что искомая плоскость может быть описана как множество всех точек r , таких что
- n ⋅ ( r − r 0 ) = 0.
(Точка здесь означает точечное произведение, а не скалярное умножение.) Расширено это становится
- a ( x − x 0 ) + b ( y − y 0 ) + c ( z − z 0 ) = 0 ,
которая является точечно-нормальной формой уравнения плоскости.[19] это всего лишь линейное уравнение:
- a x + b y + c z + d = 0 , where d = − ( a x 0 + b y 0 + c z 0 ) .
И наоборот, легко показать , что если a , b , c и d являются константами , а a, b и c не все равны нулю, то график уравнения
- a x + b y + c z + d = 0 ,
это плоскость, имеющая вектор n = ( a , b , c ) как Нормаль. это знакомое уравнение для плоскости называется общей формой уравнения плоскости.
В трехмерном пространстве линии не могут быть описаны одним линейным уравнением, поэтому они часто описываются параметрическими уравнениями:
- x = x 0 + a t \,
- y = y 0 + b t ,
- z = z 0 + c t ,
где:
- x, y и z-это все функции независимой переменной t, которая колеблется над действительными числами.
- (x 0, y 0, z 0) - любая точка на прямой.
- a , b и c связаны с наклоном линии таким образом, что вектор ( a , b , c ) параллелен линии.
Конические секции[править]
Основная статья: Коническая секция
В декартовой системе координат граф квадратичного уравнения в двух переменных всегда является коническим сечением-хотя он может быть вырожденным, и все конические сечения возникают таким образом. Уравнение будет иметь вид
- A x 2 + B x y + C y 2 + D x + E y + F = 0 with A , B , C not all zero. { не все равно ноль.}}\,
Поскольку масштабирование всех шести констант дает один и тот же локус нулей, можно рассматривать коники как точки в пятимерном проективном пространстве P 5 .
Конические сечения, описываемые этим уравнением, можно классифицировать с помощью дискриминанта
- B 2 − 4 A C . B^{2} - 4AC.\,
Если коника невырожденная, то:
- если B 2 − 4 A C < 0 -4AC, то уравнение представляет собой эллипс;
- если A = C A=C} Си B = 0 B=0, то уравнение представляет собой окружность, которая является частным случаем эллипса;
- если B 2 − 4 A C = 0 B^{2} - 4AC=0, то уравнение представляет собой параболу;
- если B 2 − 4 A C > 0 B^{2} - 4AC>0уравнение представляет собой гиперболу;
- если мы также имеем A + C = 0 A+C=0, то уравнение представляет собой прямоугольную гиперболу .
Квадрические поверхности[править]
Главная статья: Quadric поверхность
Квадрик, или квадрическая поверхность,- это двумерная поверхность в трехмерном пространстве, определяемая как локус нулей квадратичного многочлена . В координатах x 1 , x 2 , x 3 общая квадрика определяется алгебраическим уравнением
- ∑ i , j = 1 3 x i Q i j x j + ∑ i = 1 3 P i x i + R = 0.
Квадрические поверхности включают эллипсоиды (включая сферу ), параболоиды , гиперболоиды , цилиндры , конусы и плоскости .
Расстояние и угол[править]
Основные статьи: Расстояние и угол
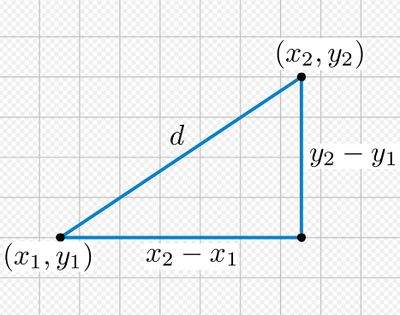
В аналитической геометрии геометрические понятия, такие как расстояние и мера угла, определяются с помощью формул . Эти определения разработаны таким образом, чтобы быть совместимыми с лежащей в их основе евклидовой геометрией . Например, при использовании декартовых координат на плоскости расстояние между двумя точками (x 1, y 1 ) и ( x 2, y 2 ) определяется по формуле
- d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 ,
что можно рассматривать как вариант теоремы Пифагора . Аналогично, угол, который линия делает с горизонталью, может быть определен формулой
- θ = arctan ( m ) ,
где m-наклон линии.
В трех измерениях расстояние задается обобщением теоремы Пифагора:
- d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 + ( z 2 − z 1 ) 2 ,
в то время как угол между двумя векторами задается точечным произведением . Точечное произведение двух евклидовых векторов A и B определяется выражением
- A ⋅ B = d e f ‖ A ‖ ‖ B ‖ cos θ ,
где θ-угол между точками A и B.
Преобразования[править]
Преобразования применяются к родительской функции, чтобы превратить ее в новую функцию с аналогичными характеристиками.
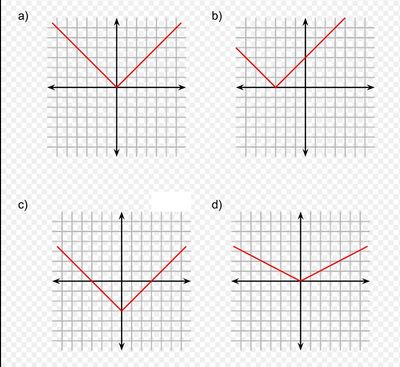
График R ( x , y ) )изменяется стандартными преобразованиями следующим образом:
- Изменение x иксна x − h x-hперемещает график в правильные h хединицы измерения.
- Изменение y yна y − k } y-kперемещение k кединиц измерения графика вверх.
- Изменение x x / bрастягивает график по горизонтали в разы b б. (подумайте о том x икс, как расширяется)
- Изменение y yна y / a y / aрастягивание графика по вертикали.
- Изменение x иксна x cos A + y sin A изменение y yдля − x sin A + y cos A - x\sin A+y\cos Aповорота графика на угол A Один.
Существуют и другие стандартные преобразования, которые обычно не изучаются в элементарной аналитической геометрии, поскольку преобразования изменяют форму объектов способами, обычно не рассматриваемыми. Перекос является примером преобразования, которое обычно не рассматривается. Дополнительную информацию смотрите в статье Википедии, посвященной аффинным преобразованиям .
Например, родительская функция y = 1 / x y=1 / xимеет горизонтальную и вертикальную асимптоты и занимает первый и третий квадранты, а все ее преобразованные формы имеют одну горизонтальную и вертикальную асимптоты и занимают либо 1-й и 3-й, либо 2-й и 4-й квадранты. В общем, если y = f ( x ) y=f (x), то его можно трансформировать
y = a f ( b ( x − k ) ) + h y=af(b(x-k))+h} y=af(b (x-k))+h.
В новой преобразованной функции a одинесть фактор, который вертикально растягивает функцию, если она больше 1, или вертикально сжимает функцию, если она меньше 1, и для отрицательных a одинзначений функция отражается на оси x икс-. То b б значение сжимает график функции по горизонтали, если больше 1, и растягивает функцию по горизонтали , если меньше 1, и, как a один, отражает функцию в оси y y-, когда она отрицательна. Значения k ки h хпредставляют h хсобой переводы, вертикальные и k кгоризонтальные. Положительные h хи k котрицательные значения означают, что функция переводится на положительный конец своей оси,а отрицательные - на отрицательный конец.
Преобразования могут быть применены к любому геометрическому уравнению, независимо от того, представляет ли уравнение функцию. Преобразования можно рассматривать как отдельные транзакции или в виде комбинаций.
Предположим, что R ( x , y ) R(x, y)это отношение на x y xyплане. Например,
- x 2 + y 2 − 1 = 0
является отношением, описывающим единичный круг.
Поиск пересечений геометрических объектов[править]
Основная статья: Пересечение (геометрия)
Для двух геометрических объектов P и Q, представленных отношениями P ( x , y ) P(x,y)} P(x, y), а Q ( x , y ) )пересечение - это совокупность всех точек ( x , y ) (x,y)} (x, y), находящихся в обоих отношениях.
Например, P Пможет быть круг с радиусом 1 и центром ( 0 , 0 ) (0,0)} (0,0): P = { ( x , y ) | x 2 + y 2 = 1 } P=\{(x, y)|x^{2}+y^{2}=1\}и Q Qможет быть круг с радиусом 1 и центром ( 1 , 0 ) : Q = { ( x , y ) | ( x − 1 ) 2 + y 2 = 1 } (1,0):Q=\{(x,y)|(x-1)^{2}+y^{2}=1\}} (1,0): Q=\{(x, y)|(x-1)^{2}+y^{2}=1\}. Пересечение этих двух кругов является совокупностью точек, которые делают оба уравнения истинными. Делает ли точка ( 0 , 0 ) (0,0)} (0,0)оба уравнения истинными? Используя ( 0 , 0 ) (0,0)} (0,0)for ( x , y ) (x,y)} (x, y), уравнение для Q Qстановится ( 0 − 1 ) 2 + 0 2 = 1 (0-1)^{2}+0^{2}=1} (0-1)^{2}+0^{2}=1или ( − 1 ) 2 = 1 (-1)^{2}=1} (-1)^{2}=1которое истинно, так ( 0 , 0 ) (0,0)} (0,0)же и в отношении Q Q. С другой стороны, все еще используется ( 0 , 0 ) (0,0)} (0,0)для ( x , y ) (x, y)уравнения для P Пстановится 0 2 + 0 2 = 1 0^{2}+0^{2}=1} 0^{2}+0^{2}=1или 0 = 1 0=1который является ложным. ( 0 , 0 ) (0,0)нет внутри P П, значит, его нет и на перекрестке.
Пересечение P Пи Q Qможет быть найдено путем решения одновременных уравнений:
- x 2 + y 2 = 1 x^{2}+y^{2}=1} x^{2}+y^{2}=1
- ( x − 1 ) 2 + y 2 = 1. (x-1)^{2}+y^{2}=1.} (x-1)^{2}+y^{2}=1.}
Традиционные методы поиска пересечений включают замену и устранение.
Подстановка: решить первое уравнение для y yв терминах x икс, а затем заменить выражение Для y yво второе уравнение:
- x 2 + y 2 = 1 x^{2}+y^{2}=1} x^{2}+y^{2}=1
- y 2 = 1 − x 2 y^{2}=1-x^{2}} y^{2}=1-x^{2}.
Затем мы подставляем это значение y 2 y^{2}} y^{2}в другое уравнение и переходим к решению для x икс:
- ( x − 1 ) 2 + ( 1 − x 2 ) = 1 (x-1)^{2}+(1-x^{2})=1} (x-1)^{2}+(1-x^{2})=1
- x 2 − 2 x + 1 + 1 − x 2 = 1 x^{2}-2x+1+1-x^{2}=1} x^{2} - 2x+1+1-x^{2}=1
- − 2 x = − 1 -2x=-1} -2x=-1
- x = 1 / 2. x=1/2.} x=1/2.}
Затем мы помещаем это значение x иксв любое из исходных уравнений и решаем для y y:
- ( 1 / 2 ) 2 + y 2 = 1 (1/2)^{2}+y^{2}=1} (1/2)^{2}+y^{2}=1
- y 2 = 3 / 4 y^{2}=3/4} y^{2}=3/4
- y = ± 3 2 . y={\frac {\pm {\sqrt {3}}}{2}}.} y={\frac {\pm {\sqrt {3}}}{2}}.}
Итак, наше пересечение имеет две точки:
- ( 1 / 2 , + 3 2 ) a n d ( 1 / 2 , − 3 2 ) . Правильно).}
Исключение: добавление (или вычитание) кратного одного уравнения к другому уравнению так, чтобы одна из переменных была исключена. Для нашего текущего примера, если мы вычитаем первое уравнение из второго, мы получим ( x − 1 ) 2 − x 2 = 0 (x-1)^{2}-x^{2}=0} (x-1)^{2}-x^{2}=0. Первое y 2 y^{2}} y^{2}уравнение вычитается из y 2 y^{2}} y^{2}второго уравнения, не оставляя никакого y y} yчлена. Переменная y y} yбыла исключена. Затем мы решаем оставшееся уравнение для x x} икс, таким же образом, как и в методе подстановки:
- x 2 − 2 x + 1 + 1 − x 2 = 1 x^{2}-2x+1+1-x^{2}=1} x^{2} - 2x+1+1-x^{2}=1
- − 2 x = − 1 -2x=-1} -2x=-1
- x = 1 / 2. x=1/2.} x=1/2.}
Затем мы помещаем это значение x иксв любое из исходных уравнений и решаем для y y:
- ( 1 / 2 ) 2 + y 2 = 1 (1/2)^{2}+y^{2}=1} (1/2)^{2}+y^{2}=1
- y 2 = 3 / 4 y^{2}=3/4} y^{2}=3/4
- y = ± 3 2 . y={\frac {\pm {\sqrt {3}}}{2}}.} y={\frac {\pm {\sqrt {3}}}{2}}.}
Итак, наше пересечение имеет две точки:
- ( 1 / 2 , + 3 2 ) a n d ( 1 / 2 , − 3 2 ) . Правильно).}
Для конических сечений в пересечении может находиться до 4 точек.
Поиск перехватов[править]
Основные статьи: X-перехват и Y-перехват
Один из видов пересечения, который широко изучается, - это пересечение геометрического объекта с осями x икс y yкоординат.
Пересечение геометрического объекта и оси y y-называется y yперехватом объекта. Пересечение геометрического объекта и оси x икс-называется x иксперехватом объекта.
Для линии y = m x + b y=mx+bпараметр b буказывает точку, в которой линия пересекает y yось. В зависимости от контекста, либо b били точка ( 0 , b ) (0,b)} (0, b)называется y y-перехват.
Касательные и нормали[править]
Касательные линии и плоскости[править]
Основная статья: Касательная
В геометрии касательная линия (или просто касательная ) к плоской кривой в данной точке - это прямая линия, которая "просто касается" кривой в этой точке. Неофициально это линия, проходящая через пару бесконечно близких точек на кривой. Более точно, прямая линия называется касательной кривой y = f ( x ) в точке x = c на кривой , если линия проходит через точку ( c, f ( c )) на кривой и имеет наклон f '(c), где f ' - производная от f . Аналогичное определение применяется к пространственным кривым и кривым в n-мерном Евклидовом пространстве .
При прохождении через точку пересечения касательной линии и кривой, называемую точкой касания , касательная линия "движется в том же направлении", что и кривая, и, таким образом, является наилучшим прямым приближением к кривой в этой точке.
Аналогично, касательная плоскость к поверхности в данной точке - это плоскость, которая "просто касается" поверхности в этой точке. Понятие касательной является одним из наиболее фундаментальных понятий в дифференциальной геометрии и было широко обобщено; см. касательное пространство .
Нормальная линия и вектор[править]
Основная статья: Нормаль (геометрия)
В геометрии Нормаль - это объект, такой как линия или вектор, перпендикулярный данному объекту. Например, в двумерном случае нормальная линия к кривой в данной точке является линией, перпендикулярной касательной к кривой в данной точке.
В трехмерном случае Нормаль поверхности или просто нормаль к поверхности в точке P-это вектор, перпендикулярный касательной плоскости к этой поверхности в точке P . Слово "Нормаль" также используется в качестве прилагательного: линия , нормальная к плоскости , нормальная составляющая силы , нормальный вектор и т. д. Понятие нормальности обобщается на ортогональность .
Смотрите также[править]
Ссылки[править]
Книги
- Boyer, Carl B. (2004) [1956], история аналитической геометрии, Dover Publications,
- Cajori, Florian (1999), A History of Mathematics, AMS,
- Джон Кейси (1885) аналитическая геометрия точек, линий, окружностей и конических сечений, ссылка из интернет-архива .
- Katz, Victor J. (1998), История математики: введение (2-е изд.), Чтение: Addison Wesley Longman,
- Struik, D. J. (1969), a Source Book in Mathematics, 1200-1800, Harvard University Press,
Статьи
- Bissell, C. C., декартова геометрия: голландский вклад
- Бойер, Карл Б. (1944), "аналитическая геометрия: Открытие ферма и Декарта", учитель математики,
- Бойер, Карл Б., Иоганн Гудд и космические координаты
- Кулидж, Дж. Л. (1948), "начало аналитической геометрии в трех измерениях", американский математический ежемесячник,
- Pecl, J., Ньютон и аналитическая геометрия