Гармоничные фигуры

Гармоничные фигуры и их проекции[править]
Гармоничная фигура одномерного пространства[править]
В одномерном пространстве любая фигура (структура) будет иметь две опорные точки. Данное утверждение легко визуально проверить – достаточно нарисовать на поверхности листа бумаги (двухмерного пространства) любую фигуру, затем повернуть лист ребром к наблюдателю. Если толщиной листа пренебречь, то мы получим одномерное пространство с нарисованной нами фигурой, которая будет выглядеть как отрезок. Любой отрезок будет всегда иметь две опорные точки. Данное утверждение можно записать следующим образом:
- a- мерность пространства, которым ограничена структура
| a |1 = 2
- 1- какая-либо структура
Иначе говоря, для определения какой-либо структуры спроектированной на одномерное пространство необходимо определить две ее опорные точки.
Гармоничная фигура двухмерного пространства[править]
Для получения гармоничной структуры двухмерного пространства необходимо провести перпендикуляр к одномерной фигуре (проекции структуры на одномерном пространстве) на длину самой фигуры, т.е. одномерная фигура «двигается» на длину самой себя по вектору являющемся перпендикуляром к ней. Оставленный при движении «след» и будет являться гармоничной фигурой двухмерного пространства.
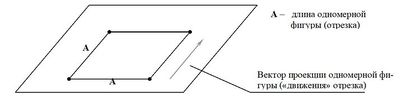
Получившаяся гармоничная фигура двухмерного пространства будет являться квадратом и соответственно иметь четыре опорные точки т.е.:
| а |2 = 4
| a |2 ≡ | a |1 ┴ | a |1 ≡ 4
Гармоничная фигура трехмерного пространства[править]
При увеличении мерности пространства на единицу гармоничная фигура получается путем проекции гармоничной фигуры предыдущей мерности на ее же длину по вектору являющимся перпендикуляром к ней и к векторам измерения предыдущей мерности, т.е.:
| a |N ≡ | a |N-1 ┴ | a |N-1
Согласно данному правилу, для получения гармоничной фигуры трехмерного пространства необходимо осуществить проекцию (движение) гармоничной фигуры двухмерного пространства на длину самой себя по вектору являющемуся перпендикуляром к векторам измерения мерности двухмерного пространства, т.е.:
| a |3 = | a |2 ┴ | a |2
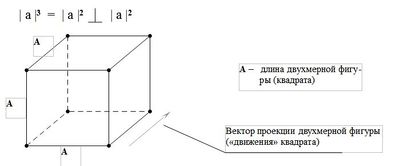
Получившийся при проекции объемный след будет являться гармоничной фигурой трехмерного пространства, т.е. кубом и иметь уже восемь опорных точек.
| a |3 ≡ | a |2 ┴ | a |2 ≡ 8
Гармоничная фигура четырехмерного пространства[править]
Аналогичным образом получаются гармоничные фигуры следующих измерений. К примеру, что бы получить гармоничную фигуру четырехмерного пространства необходимо осуществить проекцию гармоничной фигуры трехмерного пространства – куба на длину самого куба по вектору являющимся перпендикуляром к векторам измерений трехмерного пространства т.е.:
| a |4 = | a |3 ┴ | a |3
Если гармоничная трехмерная фигура (куб) наблюдается визуально только по трем ее плоскостям одновременно, то гармоничная четырехмерная фигура должна быть видна со всех сторон сразу и изнутри одновременно.
На плоскости это можно изобразить следующим образом (для удобства восприятия углы отмечены цифрами):
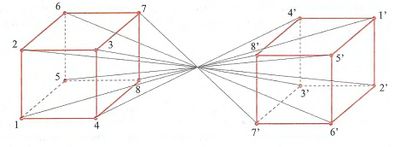
Отобразив куб таким образом, мы фактически осуществили сдвиг его по времени и получили гармоничную четырехмерную фигуру, которая имеет шестнадцать опорных точек, т.е.:
| a |4 ≡ | a |3 ┴ | a |3 ≡ 16
По данной аналогии легко выстраиваются гармоничные фигуры следующих порядков мерности их пространств.
Гармоничная фигура пятимерного пространства[править]
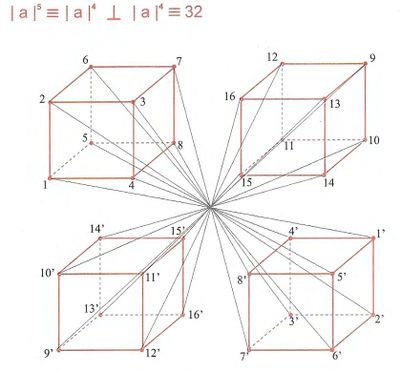
Гармоничная фигура шестимерного пространства[править]
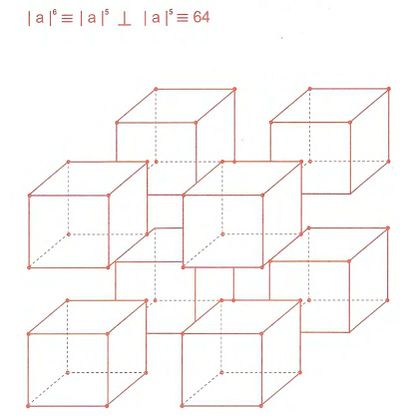
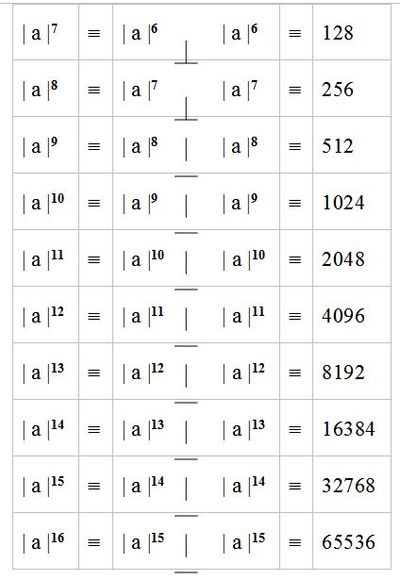
Таблица соответствий гармоничных фигур разномерных пространств с количеством их опорных точек.
| a |2 | ≡ | a |1 ┴ | a |1 | ≡ | 4 |
| a |3 | ≡ | a |2 ┴ | a |2 | ≡ | 8 |
| a |4 | ≡ | a |3 ┴ | a |3 | ≡ | 16 |
| a |5 | ≡ | a |4 ┴ | a |4 | ≡ | 32 |
| a |6 | ≡ | a |5 ┴ | a |5 | ≡ | 64 |