Многозначная логика

Материал из wikixw
Перейти к навигации Перейти к поиску

В логикемногозначная логика (также многозначная или многозначная логика) - это пропозициональное исчисление, в котором существует более двух истинностных значений. Традиционно в логическом исчислении Аристотелябыло только два возможных значения (т. е. "истинно" и "ложно") для любого предложения. Классическая двузначная логика может быть расширена до n-значной логики для n больше 2. Наиболее популярными в литературе являются трехзначные (например, Лукасевич и Клейн, которые принимают значения "истинно"," ложно "и" неизвестно"), конечнозначные (конечно-многозначные) с более чем тремя значениями и бесконечнозначные (бесконечно-многозначные), такие как нечеткая логика и вероятностная логика.

История[править]

Первым известным классическим логиком, который не до конца принял закон исключенного среднего, был Аристотель (которого, по иронии судьбы, также принято считать первым классическим логиком и "отцом логики"). Аристотель признавал , что не все его законы применимы к будущим событиям (De Interpretatione, гл. IX), но он не создал систему многозначной логики, чтобы объяснить это изолированное замечание. До начала XX века более поздние логики следовали аристотелевской логике, которая включает или предполагает закон исключенной середины.

20-й век вернул идею многозначной логики. Польский логик и философ Ян Лукашевич начал создавать системы многозначной логики в 1920 году, используя третье значение, "возможное", чтобы иметь дело с парадоксом Аристотеля о морском сражении. Между тем американский математик Эмиль л. пост (1921) также ввел формулировку дополнительных степеней истинности с n ≥ 2, где n-значения истинности. Позже Ян Лукасевич и Альфред Тарский вместе сформулировали логику о n истинностных значениях, где n ≥ 2. В 1932 году Ганс Райхенбах сформулировал логику многих истинностных значений, где n→∞. Курт Гедель в 1932 году показал , что интуиционистская логика не является конечно-многозначной логикой, и определил систему логик Геделя, промежуточную между классической и интуиционистской логикой; такие логики известны как промежуточные логики.

Примеры[править]

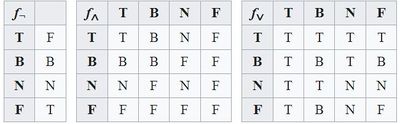
Основные статьи: трехзначная логика, четырехзначнаялогика и девятизначная логика Kleene (strong) K3 и Priest logic P3 Клина "(сильная) логика неопределенности " K3 (иногда K 3 S ) и "логика парадокса" священника добавляют третье" неопределенное "или" неопределенное " значение истинности I. Функции истинности для отрицания (), конъюнкции (conjunction), дизъюнкции (impl), импликации (→K) и бикондиции (↔K) задаются следующим образом:

Различие между этими двумя логиками заключается в том, как определяются тавтологии. В K3 только T является обозначенным значением истинности, в то время как в P3 и T, и I являются (логическая формула считается тавтологией, если она вычисляется до обозначенного значения истинности). В логике Клина я могу быть истолкован как "недетерминированный", не являющийся ни истинным, ни ложным, в то время как в логике приста я могу быть истолкован как" сверхдетерминированный", являющийся одновременно истинным и ложным. K3 не имеет тавтологий, в то время как P3 имеет те же тавтологии, что и классическая двузначная логика.

Внутренняя трехзначная логика Бочвара[править]

Другая логика-это "внутренняя" трехзначная логика Бочвара B 3 I }, также называемая слабой трехзначной логикой Клина. За исключением отрицания и бикондиционирования, все его таблицы истинности отличаются от приведенных выше.

Промежуточное значение истинности в "внутренней" логике Бочвара можно описать как "заразное", поскольку оно распространяется в Формуле независимо от значения любой другой переменной.

Логика белнапа (B4)[править]

Логика белнапа B4 объединяет K3 и P3. Сверхдетерминированное значение истинности здесь обозначается как B, а недетерминированное значение истинности-как N.


Логика Геделя Gk и G∞[править]

В 1932 году Гедель определил семейство G k {многозначных логик с конечным числом истинностных значений 0 , 1 k − 1 , 2 k − 1 , … k − 2 k − 1 , 1 например G 3 }имеет истинностные значения 0 , 1 2 , 1 }, 1и G 4 }имеет 0 , 1 3 , 2 3 , 1 }, 1. Подобным же образом он определил логику с бесконечно большим числом истинностных значений G ∞ }, в которой истинностными значениями являются все действительные числа в интервале [ 0 , 1 ] [0,1]. Обозначенное значение истинности в этих логиках равно 1.

Конъюнкция ∧ \клин и дизъюнкция ∨ } \ВЭ определяются соответственно как минимум и максимум операндов: 

   u ∧ v := min { u , v }
  • u ∨ v := max { u , v }

Отрицание ¬ G и импликация → G {}определяются следующим образом: 

   ¬ G u = { 1 , if  u = 0 0 , if  u > 0 u → G v = { 1 , if  u ≤ v v , if  u > v


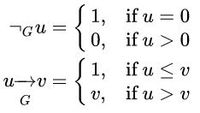
Логика Геделя полностью аксиоматизируема, то есть можно определить логическое исчисление, в котором все тавтологии доказуемы.

Логика Лукасевича Lv и L∞[править]

Импликация → L и отрицание ¬ L были определены Яном Лукашевичем через следующие функции: 

   ¬ L u := 1 − u 

   u → L v := min { 1 , 1 − u + v }

Сначала Лукасевич использовал это определение в 1920 году для своей трехзначной логики L 3 }с истинностными значениями 0 , 1 2 , 1 , 1. В 1922 году он разработал логику с бесконечно большим числом значений L ∞ }, в которой истинностные значения охватывали действительные числа в интервале [ 0 , 1 ] . В обоих случаях указанное значение истинности было равно 1.

Приняв значения истинности, определенные таким же образом , как и для логик Геделя 0 , 1 v − 1 , 2 v − 1 , … , v − 2 v − 1 , 1 1, можно создать конечнозначное семейство логик L v , вышеописанных L ∞ }и логик L ℵ 0 , в которых значения истинности задаются рациональными числами в интервале [ 0 , 1 ] . Множество тавтологий В L ∞ }и L ℵ 0 тождественно.

Логика продукта Π[править]

В продуктовой логике мы имеем истинностные значения в интервале [ 0 , 1 ] } [0,1], конъюнкции ⊙ odot } \одот и импликации → Π xrightarrow}, определяемые следующим образом[7] 

   u ⊙ v := u v odot v:=uv} u\odot v:=uv

    u→ Π v := { 1 , if  u ≤ v v u , if  u > v

Кроме того, существует отрицательное обозначенное значение 0 ¯ }, которое обозначает понятие ложь. Через это значение можно определить отрицание ¬ Π underset и дополнительную конъюнкцию ∧ Π underset wedge клин следующим образом: 

   ¬ Π u := u → Π 0 ¯ {\overline 

   u ∧ Π v := u ⊙ ( u → Π v )

Post logics Pm[править]

В 1921 году пост определил семейство логик P m (как и в L v G_{k}) истинностными значениями 0 , 1 m − 1 , 2 m − 1 , … , m − 2 m − 1 , 1 , 1. Отрицание ¬ P , конъюнкция ∧ P и дизъюнкция ∨ P }определяются следующим образом: 

   ¬ P u := { 1 , if  u = 0 u − 1 m − 1 , if  u ≠ 0 

   u ∧ P v := min { u , v }

   u ∨ P v := max { u , v }

Розовая логика[править]

В 1951 году Алан Роуз определил еще одно семейство логик для систем, истинностные значения которых образуют решетки. ("Системы логики, истинностные значения которых образуют решетки", матем. Annalen, vol. 123, декабрь 1951, стр. 152-165; источник).

Семантика[править]

Матричная семантика (логические матрицы)[править]

См. раздел Логическая матрица

Отношение к классической логике[править]

Логики обычно представляют собой системы, предназначенные для кодификации правил сохранения некоторого семантического свойства предложений через преобразования. В классической логикеэто свойство называется " истиной."В действительном аргументе истинность производного предложения гарантируется, если посылки совместно истинны, потому что применение действительных шагов сохраняет свойство. Однако это свойство не обязательно должно быть свойством "истины"; вместо этого оно может быть каким-то другим понятием.

Многозначные логики предназначены для сохранения свойства обозначаемости (или обозначаемости). Поскольку существует более двух значений истинности, правила вывода могут быть предназначены для сохранения большего, чем просто то, что соответствует (в соответствующем смысле) истине. Например, в трехзначной логике иногда обозначаются два наибольших истинностных значения (когда они представлены, например, в виде положительных целых чисел), и правила вывода сохраняют эти значения. Именно, веский аргумент будет таким,что ценность совместно взятых посылок всегда будет меньше или равна заключению.

Например, сохраненное свойство может быть оправданием, основополагающим понятием интуиционистской логики. Таким образом, пропозиция не является истинной или ложной; напротив, она обоснована или ошибочна. Ключевое различие между обоснованием и истиной в данном случае состоит в том, что закон исключенной середины не имеет силы: предложение, которое не является ошибочным, не обязательно оправдано; вместо этого, только не доказано, что оно ошибочное. Ключевым отличием является определенность сохраняемого свойства: можно доказать, что Р оправдано, что Р является ущербным или не может доказать ни то, ни другое. Действительный аргумент сохраняет оправдание через преобразования, поэтому предложение, производное от обоснованных предложений, все еще оправдано. Однако в классической логике существуют доказательства, которые зависят от закона исключенной середины; поскольку этот закон не применим в рамках данной схемы, существуют предложения, которые не могут быть доказаны таким образом.

=Тезис Сушко[править]

См. также: Принцип бивалентности § Тезис Сушко

Функциональная полнота многозначных логик[править]

Функциональная полнота-это термин, используемый для описания специального свойства конечных логик и алгебр. Набор логических связей считается функционально полным или адекватным тогда и только тогда, когда его набор связей может быть использован для построения формулы, соответствующей каждой возможной функции истинности. Адекватной алгеброй является такая, в которой каждое конечное отображение переменных может быть выражено некоторой композицией его операций.

Классическая логика: CL = ({0,1}, , →, ∨, ∧, ↔) функционально полна, тогда как ни одна логика Лукашевича или бесконечно многозначная логика не обладает этим свойством.

Мы можем определить конечнозначную логику как Ln ({1, 2, ..., n} ƒ1, ..., ƒm), где n ≥ 2-заданное натуральное число. Пост (1921) доказывает, что если предположить, что логика способна производить функцию любой модели m-го порядка, то в адекватной логике L n существует некоторая соответствующая комбинация связок, которая может производить модель порядка m+1 .

Приложения[править]

Известные приложения многозначной логики можно условно разделить на две группы. первая группа использует многозначную логическую область для более эффективного решения бинарных задач. Например, хорошо известный подход к представлению булевой функции с несколькими выходами состоит в том, чтобы рассматривать ее выходную часть как единственную многозначную переменную и преобразовывать ее в характеристическую функцию с одним выходом (в частности, индикаторную функцию). Другие области применения многозначной логики включают проектирование программируемых логических массивов (PLAs) с входными декодерами, оптимизацию конечных автоматов, тестирование и верификацию.

Вторая группа предназначена для проектирования электронных схем, использующих более двух дискретных уровней сигналов, таких как многозначные запоминающие устройства, арифметические схемы и полевые программируемые вентильные матрицы (ПЛИС). Многозначные схемы имеют ряд теоретических преимуществ перед стандартными бинарными схемами. Например, микросхема включения и выключения интерконнекта может быть уменьшена, если сигналы в цепи принимают четыре или более уровней, а не только два. При проектировании памяти хранение двух вместо одного бита информации на ячейку памяти удваивает плотность памяти в том же размере матрицы. Приложения, использующие арифметические схемы, часто выигрывают от использования альтернатив двоичным системам счисления. Например, остаточные и избыточные системы счисления могут уменьшить или устранить пульсацию сквозных переносов которые участвуют в обычном двоичном сложении или вычитании, что приводит к высокоскоростным арифметическим операциям. Эти системы счисления имеют естественную реализацию с использованием многозначных схем. Однако практичность этих потенциальных преимуществ в значительной степени зависит от наличия схемных реализаций, которые должны быть совместимы или конкурентоспособны с современными стандартными технологиями. Помимо помощи в проектировании электронных схем, многозначная логика широко используется для проверки схем на наличие неисправностей и дефектов. В основном всем известная автоматическая генерация тестовых паттернов Алгоритмы (ATG), используемые для тестирования цифровых схем, требуют имитатора, который может разрешать 5-значную логику (0, 1, x, D, D'). дополнительные значения—x, D и D' - представляют собой

(1) неизвестное/неинициализированное,

(2) 0 вместо 1 и

(3) 1 вместо 0.

Исследовательские центры[править]

Международный симпозиум IEEE по многозначной логике (ISMVL) проводится ежегодно с 1970 года. Он в основном обслуживает приложения в области цифрового проектирования и верификации.[15] существует также Журнал многозначной логики и мягких вычислений.[16]

См. также[править]

Портал:Философский Портал:Психологический

Математическая логика

Философская логика

Цифровая логика

Дальнейшее чтение[править]

Общая информация

  • Augusto, Luis M. (2017). Многозначные логики: математическое и вычислительное введение. London: College Publications. 340 страниц. . Веб-страница
  • Béziau J.-Y. (1997), что такое многозначная логика ? Труды 27-го Международного симпозиума по многозначной логике, IEEE Computer Society, Лос-Аламитос, стр. 117-121.
  • Malinowski, Gregorz, (2001), Many-Valued Logics, in Goble, Lou, ed., Руководство Блэкуэлла по философской логике. Блэквелл.
  • Bergmann, Merrie (2008), An introduction to many-valued and fuzzy logic: semantics, Algebra, and derivation systems, Cambridge University Press, ISBN 978-0-521-88128-9
  • Cignoli, R. L. O., D'Ottaviano, I, M. L., Mundici, D., (2000). Алгебраические основы многозначных рассуждений. Kluwer.
  • Malinowski, Grzegorz (1993). Многозначная логика. Кларендон Пресс. .
  • Готвальд, Трактат о многозначных логиках. Исследования в области логики и вычислений, т. 9, Research Studies Press: Baldock, Hertfordshire, England, 2001.
  • Gottwald, Siegfried (2005). "Многозначные логики" (PDF). Архивирован с оригинала на 2016-03-03.
  • Miller, D. Michael; Thornton, Mitchell A. (2008). Многозначная логика: понятия и представления. Лекции по синтезу цифровых схем и систем. 12. Издательство "Морган И Клейпул". .
  • Hájek P., (1998), Метаматематика нечеткой логики. Kluwer. (Нечеткая логика понимается как многозначная логика sui generis.)

Специфический

  • Александр Зиновьев, философские проблемы многозначной логики, издательство Д. Рейделя, 169 С., 1963.
  • Приор А. 1957, время и модальность. Издательство Оксфордского университета, основанное на его лекциях Джона Локка 1956 года
  • Goguen J. A. 1968/69, the logic of inact concepts, Synthese, 19, 325-373.
  • Chang C. C. and Keisler H. J. 1966. Теория Непрерывной Модели, Принстон, Издательство Принстонского Университета.
  • Герла Г. 2001, нечеткая логика: математические инструменты для приближенного рассуждения, Kluwer Academic Publishers, Dordrecht.
  • Павелка Дж. 1979, о нечеткой логике I: многозначные правила вывода, Zeitschr. f. математика. Logik und Grundlagen d. Math., 25, 45–52.
  • Metcalfe, George; Olivetti, Nicola; Dov M. Gabbay (2008). Теория доказательств для нечетких логик. Прыгун. . Охватывает также теорию доказательства многозначных логик в традиции Хаджека.
  • Hähnle, Reiner (1993). Автоматическая дедукция в многозначных логиках. Кларендон Пресс.
  • Азеведо, Франсиско (2003). Решение ограничений по многозначным логикам: применение к цифровым схемам. IOS Press.
  • Болк, Леонард; Боровик, Петр (2003). Многозначные логики 2: автоматизированные рассуждения и практические приложения. Прыгун.
  • Станкович, Радомир С.; Астола, Яакко Т.; Морага, Клаудио (2012). Представление многозначных логических функций. Издательство "Морган И Клейпул". doi:10.2200/S00420ED1V01Y201205DCS037.
  • Абрамович, Мирон; Брейер, Мелвин А.; Фридман, Артур Д. (1994). Тестирование цифровых систем и тестируемый дизайн. New York: Computer Science Press

Пруф[править]

//sqig.math.ist.utl.pt/

Источник — https://wikixw.ru/index.php?title=Многозначная_логика&oldid=21164