Октаэдр

Описание[править]
Рисунок 74: Графическая интерпретация алгоритма строения развертки основы мироздания – октаэдр - шаг первый: «Десять невыразимых Сефирот имеют десять бесконечностей:
- бесконечное начало и бесконечный конец,
- бесконечное добро и бесконечное зло,
- бесконечная высота и бесконечная глубина,
- бесконечный Восток и бесконечный Запад,
- бесконечный Север и бесконечный Юг,
- и над всеми Единый Господь Бог, истинный Царь. Он правит всеми и вся из Своего священного обиталища из века в век» (каббала. Сефер Ецира: 5.).
Для альбома см. Octahedron (альбом).
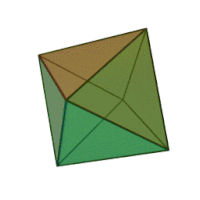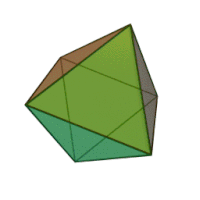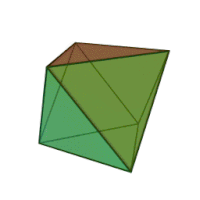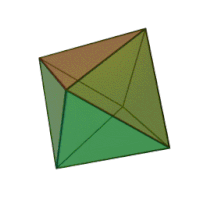
В геометрии октаэдр (множественное число: октаэдры, октаэдры) представляет собой многогранник с восемью гранями. Термин чаще всего используется для обозначения правильного октаэдра, платонова твердого тела, состоящего из восьми равносторонних треугольников, четыре из которых сходятся в каждой вершине.
Правильный октаэдр - это двойной многогранник куба. Это выпрямленный тетраэдр. Это квадратная бипирамида в любой из трех ортогональных ориентаций. Это также треугольная антипризма в любой из четырех ориентаций.
Октаэдр - это трехмерный случай более общей концепции перекрестного многогранника.
Правильный октаэдр - это 3 шара в метрике Манхэттена (ℓ 1).
Правильный октаэдр[править]
Размеры[править]
Если длина ребра правильного октаэдра равна a, то радиус описанной сферы (той, которая касается октаэдра во всех вершинах) равен
r_{u}={\frac {\sqrt {2}}{2}}a\approx 0.707\cdot a} r_{u}={\frac {\sqrt {2}}{2}}a\приблизительно 0,707\cdot a}
а радиус вписанной сферы (касательной к каждой из граней октаэдра) равен
r_{i}={\frac {\sqrt {6}}{6}}a\approx 0.408\cdot a} r_{i}={\frac {\sqrt {6}}{6}}a\приблизительно 0,408\cdot a}
в то время как средний радиус, который касается середины каждого ребра, равен
r_{m}={\tfrac {1}{2}}a=0.5\cdot a r_{m}={\tfrac {1}{2}}a=0,5\cdot a} Ортогональные проекции
Октаэдр имеет четыре специальных ортогональных проекции: центрированную, на ребро, вершину, грань и нормальную к грани. Вторая и третья соответствуют плоскостям B2 и A2 Кокстера.
Сферическая черепица[править]
Октаэдр также может быть представлен в виде сферической плитки и спроецирован на плоскость с помощью стереографической проекции. Эта проекция является конформной, сохраняя углы, но не площади или длины. Прямые линии на сфере проецируются на плоскость в виде дуг окружности.
Декартовы координаты[править]
Октаэдр с длиной ребра √2 можно поместить так, чтобы его центр находился в начале координат, а вершины - на осях координат; тогда декартовы координаты вершин будут
( ±1, 0, 0 );
- ( 0, ±1, 0 );
- ( 0, 0, ±1 ).
В декартовой системе координат x–y–z октаэдр с центральными координатами (a, b, c) и радиусом r представляет собой множество всех точек (x, y, z), таких, что
\left|x-a\right|+\left|y-b\right|+\left|z-c\right|=r.}\left|x-a\right|+\left|y-b\right|+\left|z-c\right|=r.
Площадь и объем[править]
Площадь поверхности A и объем V правильного октаэдра с длиной ребра a равны:
A=2{\sqrt {3}}a^{2}\approx 3.464a^{2}}A=2{\sqrt {3}}a^ {2}\ приблизительно 3,464a ^ {2}
V={\frac {1}{3}}{\sqrt {2}}a^{3}\approx 0.471a^{3}}V= {\ frac {1}{3}}{\sqrt {2}}a ^ {3} \ приблизительно 0,471а ^ {3}
Таким образом, объем в четыре раза больше, чем у обычного тетраэдра с той же длиной ребра, а площадь поверхности в два раза (потому что у нас 8, а не 4 треугольника).
Если октаэдр был растянут так, что он подчиняется уравнению
\left|{\frac {x}{x_{m}}}\right|+\left|{\frac {y}{y_{m}}}\right|+\left|{\frac {z}{z_{m}}}\right|=1,}\left|{\frac {x}{x_{m}}}\right|+\left|{\frac {y}{y_{m}}}\right|+\left|{\frac {z}{z_{m}}}\right|=1, формулы для площади поверхности и объема расширяются, чтобы стать
A=4\,x_{m}\,y фракция {1}{y_{m}^{2}}}+{\frac {1}{z_{m}^{2}}}}},
V={\frac {4}{3}}\,x_{m}\,y_{m}\,z_{m}.}V= {\frac {4}{3}}\,x_{m}\,y_{m}\,z_{m}.
Кроме того, тензор инерции растянутого октаэдра равен
I={\begin{bmatrix}{\frac {1}{10}}m(y_{m}^{2}+z_{m}^{2})&0&0\\0&{\frac {1}{10}}m(x_{m}^{2}+z_{m}^{2})&0\\0&0&{\frac {1}{10}}m(x_{m}^{2}-y_{m}^{2})\end{bmatrix}}.} фракция \ фракция конец{матрица}}.} Они сводятся к уравнениям для правильного октаэдра, когда
{\displaystyle x_{m}=y_{m}=z_{m}=a\,{\frac {\sqrt {2}}{2}}.}x_{m}=y_{m}=z_{m}=a\,{\frac {\sqrt {2}}{2}}. Геометрические соотношения Используя стандартную номенклатуру для твердых тел Джонсона, октаэдр будет называться квадратной бипирамидой.
Двойной[править]
Октаэдр - это двойной многогранник куба.

Если октаэдр с длиной ребра {\displaystyle =a} =a}вписан в куб, то длина ребра куба ={\sqrt {2}}a}{\displaystyle ={\sqrt {2}}a}.
Стелляция[править]
Внутренняя часть соединения двух двойных тетраэдров представляет собой октаэдр, и это соединение, называемое восьмигранником стеллы, является его первым и единственным стеллаж. Соответственно, правильный октаэдр является результатом отсечения от правильного тетраэдра четырех правильных тетраэдров вдвое меньшего линейного размера (т.е. выпрямления тетраэдра). Вершины октаэдра лежат в середине ребер тетраэдра, и в этом смысле он относится к тетраэдру так же, как кубоктаэдр и икосидодекаэдр относятся к другим платоновым телам.
Короткий октаэдр[править]
Можно также разделить ребра октаэдра в соотношении золотого сечения, чтобы определить вершины икосаэдра. Это делается путем первого размещения векторов вдоль ребер октаэдра таким образом, чтобы каждая грань была ограничена циклом, затем аналогичным образом разбивая каждое ребро на золотую середину вдоль направления его вектора. Существует пять октаэдров, которые определяют любой данный икосаэдр таким образом, и вместе они определяют правильное соединение. Икосаэдр, полученный таким образом, называется тупым октаэдром.
Мозаичные=[править]
Октаэдры и тетраэдры можно чередовать, образуя вершину, ребро и грань - однородную тесселяцию пространства. Это и регулярная мозаика кубов являются единственными такими однородными сотами в трехмерном пространстве.
Характерная ортосхема[править]
Как и все правильные выпуклые многогранники, октаэдр может быть разбит на целое число непересекающихся ортосхем, имеющих одинаковую форму, характерную для многогранника. Характерная ортосхема многогранника является фундаментальным свойством, поскольку многогранник генерируется отражениями в гранях его ортосхемы. Ортосхема встречается в двух киральных формах, которые являются зеркальными отражениями друг друга. Характерной ортосхемой правильного многогранника является четырехпрямоугольный неправильный тетраэдр.
Грани характерного тетраэдра октаэдра лежат в зеркальных плоскостях симметрии октаэдра. Октаэдр уникален среди платоновых тел тем, что имеет четное число граней, сходящихся в каждой вершине. Следовательно, это единственный член этой группы, обладающий среди своих зеркальных плоскостей некоторыми, которые не проходят ни через одну из его граней. Группа симметрии октаэдра обозначается B3. Октаэдр и его двойной многогранник, куб, имеют одну и ту же группу симметрии, но разные характеристические тетраэдры.
Характеристический тетраэдр правильного октаэдра можно найти с помощью канонического расчленения [1] правильного октаэдраУзел CDel 1.pngCDel 3.pngУзел CDel.pngCDel 4.pngУзел CDel.png, которое подразделяет его на 48 таких характерных ортосхем, Узел CDel.pngCDel 3.pngУзел CDel.pngCDel 4.pngУзел CDel.pngокружающих центр октаэдра. Три ортосхемы с левой и три ортосхемы с правой стороны встречаются в каждой из восьми граней октаэдра, шесть ортосхем в совокупности образуют трехпрямоугольный тетраэдр: треугольную пирамиду с гранью октаэдра в качестве равностороннего основания и ее вершиной в виде куба в центре октаэдра
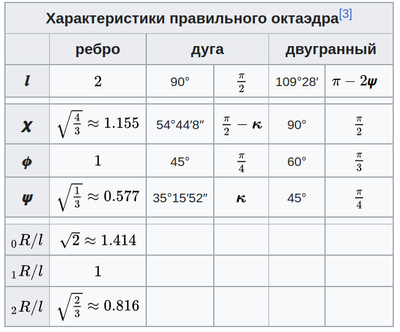
Если длина ребра октаэдра 𝒍 = 2, то шесть ребер его характерного тетраэдра имеют длины {\{4}{3}}}(внешняя грань прямоугольного треугольника, характерный треугольник 𝟀, 𝝓, 𝟁 октаэдра), плюс {\di}}}(ребра, являющиеся характерными радиусами октаэдра). Путь с тремя ребрами вдоль ортогональных ребер ортосхемы{\displaystyle 1}1, {\tfrac {\tfrac {1}{3}}}}, {\tfrac {2}{3}}}}{\sqrt {\tfrac {2}{3}}}}, сначала от вершины октаэдра к центру ребра октаэдра, затем поворачивается на 90 ° к центру грани октаэдра, затем поворачивается на 90 ° к центру октаэдра. Ортосхема имеет четыре разные грани прямоугольного треугольника. Внешняя грань представляет собой треугольник 90-60-30, который составляет одну шестую части грани октаэдра. Тремя внутренними гранями октаэдра являются: треу\ {\sqrt {\tfrac {2}{3}}}}{\ {\sqrt {\tfrac {2}{3}}}}, и прямоугольный треугольник с ребрами {\sqrt {\tfrac {4}{3}}}}{{\sqrt {\tfrac {4}{3}}}}, {\sqrt {2}}}{\sqrt {2}}, {\ {\sqrt {\tfrac {2}{3}}}}{ {\sqrt {\tfrac {2}{3}}}}.
Топология[править]
Октаэдр 4-связный, что означает, что для разъединения оставшихся вершин требуется удаление четырех вершин. Это один из четырех 4-связных симплициальных хорошо покрытых многогранников, что означает, что все максимальные независимые множества его вершин имеют одинаковый размер. Другими тремя многогранниками, обладающими этим свойством, являются пятиугольная дипирамида, тупой дисфеноид и неправильный многогранник с 12 вершинами и 20 треугольными гранями.[4]
Сети[править]
Правильный октаэдр имеет одиннадцать расположений сеток.
Огранка[править]
Равномерный тетрагексаэдр представляет собой четырехгранную симметричную грань правильного октаэдра, имеющую общее расположение ребер и вершин. Он имеет четыре треугольные грани и 3 центральных квадрата.
Равномерная окраска и симметрия[править]
Существует 3 однородных раскраски октаэдра, названных по цветам треугольных граней, окружающих каждую вершину: 1212, 1112, 1111.
Группой симметрии октаэдра является Oh 48-го порядка, трехмерная гипероктаэдрическая группа. Подгруппы этой группы включают D 3d (порядок 12), группу симметрии треугольной антипризмы; D 4h (порядок 16), группу симметрии квадратной бипирамиды; и Td (порядок 24), группу симметрии выпрямленного тетраэдра. Эти симметрии могут быть подчеркнуты различной окраской граней.
Неправильные октаэдры[править]
Следующие многогранники комбинаторно эквивалентны правильному многограннику. Все они имеют шесть вершин, восемь треугольных граней и двенадцать ребер, которые один к одному соответствуют элементам правильного октаэдра.
Треугольные антипризмы: две грани равносторонние, лежат в параллельных плоскостях и имеют общую ось симметрии. Остальные шесть треугольников равнобедренные. Тетрагональные бипирамиды, в которых по крайней мере один из экваториальных четырехугольников лежит на плоскости. Правильный октаэдр является частным случаем, в котором все три четырехугольника являются плоскими квадратами. Многогранник Шенхардта, невыпуклый многогранник, который нельзя разбить на тетраэдры без введения новых вершин. Октаэдр Брикара, невыпуклый самопересекающийся гибкий многогранник В более общем смысле октаэдром может быть любой многогранник с восемью гранями. Правильный октаэдр имеет 6 вершин и 12 ребер, минимум для октаэдра; неправильные октаэдры могут иметь до 12 вершин и 18 ребер.[5] Существует 257 топологически различных выпуклых октаэдров, исключая зеркальные изображения. Более конкретно, существуют 2, 11, 42, 74, 76, 38, 14 для октаэдров с 6-12 вершинами соответственно. (Два многогранника являются "топологически различными", если они имеют внутренне различное расположение граней и вершин, так что невозможно исказить один вдругой просто путем изменения длины ребер или углов между ребрами или гранями.)
Некоторые более известные неправильные октаэдры включают следующие:
Шестиугольная призма: Две грани параллельны правильным шестиугольникам; шесть квадратов соединяют соответствующие пары ребер шестиугольника. Семиугольная пирамида: одна грань представляет собой семиугольник (обычно правильный), а остальные семь граней представляют собой треугольники (обычно равнобедренные). Невозможно, чтобы все треугольные грани были равносторонними. Усеченный тетраэдр: четыре грани тетраэдра усечены, чтобы стать правильными шестиугольниками, и есть еще четыре равносторонние треугольные грани, где каждая вершина тетраэдра была усечена. Тетрагональный трапецоэдр: восемь граней являются конгруэнтными воздушными змеями. Восьмиугольный осоэдр: вырождается в евклидовом пространстве, но может быть реализован сферически.
Октаэдры в физическом мире[править]
Октаэдры в природе[править]
Природные кристаллы алмаза, квасцов или флюорита обычно имеют октаэдрическую форму, в виде заполняющих пространство четырехгранно-октаэдрических сот. Пластины из сплава камасита в октаэдритовых метеоритах расположены параллельно восьми граням октаэдра. Многие ионы металлов координируют шесть лигандов в октаэдрической или искаженной октаэдрической конфигурации. Widmanstätten patterns в никель-железо кристаллы
Октаэдры в искусстве и культуре[править]


Особенно в ролевых играх это твердое тело известно как "d8", одна из наиболее распространенных многогранных костей.
- Если каждое ребро октаэдра заменить резистором в один Ом , сопротивление между противоположными вершинами равно
2/1
Ом, и что между соседними вершинами
12/5
Ом.
- Шесть музыкальных нот могут быть расположены на вершинах октаэдра таким образом, что каждое ребро представляет согласную диаду, а каждая грань представляет согласную триаду; см. шестиугольник.
Тетраэдрическая восьмигранная ферма[править]
Пространственный каркас из чередующихся тетраэдров и полуоктаэдров, полученных из четырехгранно-октаэдрических сот, был изобретен Бакминстером Фуллером в 1950-х годах. Обычно считается самой прочной строительной конструкцией, способной противостоять консольным нагрузкам.
Связанные многогранники[править]
Октаэдр является одним из семейства однородных многогранников, связанных с кубом.
Это также один из простейших примеров гиперсимплекса, многогранника, образованного определенными пересечениями гиперкуба с гиперплоскостью.
Октаэдр топологически связан как часть последовательности правильных многогранников с символами Шлефли {3,n}, продолжающимися в гиперболической плоскости.
Тетратетраэдр[править]

Правильный октаэдр также можно считать выпрямленным тетраэдром - и его можно назвать тетратетраэдром. Это можно показать с помощью 2-цветной модели лица. При такой окраске октаэдр имеет тетраэдрическую симметрию.
Сравните эту последовательность усечения между тетраэдром и его двойственным:
Вышеуказанные формы также могут быть реализованы в виде срезов, ортогональных длинной диагонали тессеракта. Если эта диагональ ориентирована вертикально с высотой 1, то первые пять срезов выше расположены на высотах r,
3/8, 1/2, 8/5
- и s, где r - любое число в диапазоне 0 < r ≤
- 4/1, а s - любое число в диапазоне
- 4/3 ≤ s < 1.
Октаэдр как тетратетраэдр существует в последовательности симметрий квазирегулярных многогранников и разбиений с конфигурациями вершин (3.n)2, переходящих от разбиений сферы к евклидовой плоскости и к гиперболической плоскости. С симметрией обозначения орбифолда * n 32 все эти разбиения являются конструкциями Витхоффа в фундаментальной области симметрии с образующими точками в правом угловом углу области.[
- Правильный октаэдр можно увеличить до тетраэдра, добавив 4 тетраэдра на чередующихся гранях. Добавление тетраэдров ко всем 8 граням создает звездчатый октаэдр.
Тригональная антипризма[править]
Как тригональная антипризма, октаэдр относится к семейству гексагональных двугранных симметрий.
Квадратная бипирамида[править]
Другие связанные многогранники Усечение двух противоположных вершин приводит к квадратному раздвоению.
Октаэдр может быть сгенерирован как случай 3D суперэллипсоида со всеми значениями экспоненты, равными 1.
Смотри также[править]
Октаэдрическое число * Центрированное восьмигранное число * Вращающийся октаэдр * Стелла восьмигранная * Октаэдр Триакиса * Октаэдр Гексакиса * Усеченный октаэдр * Октаэдрическая молекулярная геометрия *