Отношение шансов
С коэффициентом соотношении (или)- это статистический показатель , который характеризует силу связи между двумя событиями A и B. коэффициент коэффициент определяется как отношение шансов в присутствии Б и шансы в отсутствии Б, или, что эквивалентно (в силу симметрии), соотношение коэффициентов B в наличии и шансы на Б в отсутствие А. Два события являются независимыми тогда и только тогда, когда или равно 1, то есть шансы одного события одинаковы либо при наличии, либо при отсутствии другого события. Если ОР больше 1, то А и в связаны (коррелированы) в том смысле, что по сравнению с отсутствием в присутствие в повышает шансы а, а симметрично присутствие А повышает шансы Б. И наоборот, если ОР меньше 1, то А и в отрицательно коррелированы, и наличие одного события уменьшает шансы другого события.
Обратите внимание, что отношение шансов симметрично в двух событиях, и нет никакого подразумеваемого причинного направления (корреляция не подразумевает причинности): положительное или не устанавливает, что B вызывает A, или что A вызывает B.
Две схожие статистические величины, которые часто используются для количественной оценки ассоциаций, - это коэффициент риска (RR) и абсолютное снижение риска (ARR). Часто наибольший интерес представляет параметр RR, представляющий собой отношение вероятностей, аналогичных коэффициентам, используемым в ОР. Однако имеющиеся данные часто не позволяют вычислить RR или ARR, но позволяют вычислить OR, как в исследованиях case-control, как описано ниже. С другой стороны, если одно из свойств (А или В) является достаточно редким (в эпидемиологии это называется предположением о редком заболевании), то ор приблизительно равен соответствующему RR.
ОР играет важную роль в логистической модели.
Определение и основные свойства[править]
Мотивирующий пример, в контексте предположения о редком заболевании[править]
Представьте себе, что существует редкое заболевание, поражающее, скажем, только одного из многих тысяч взрослых в стране. Представьте себе, что мы подозреваем, что, подвергаясь воздействию чего-то (скажем, имея определенный вид травмы в детстве), человек с большей вероятностью может развить эту болезнь во взрослом возрасте. Наиболее информативной вещью для вычисления будет коэффициент риска, RR. Чтобы сделать это в идеальном случае, для всех взрослых в популяции нам нужно было бы знать, подвергались ли они (а) воздействию травмы в детстве и (Б) развились ли у них заболевания во взрослом возрасте. Из этого мы извлекли бы следующую информацию: общее число людей, подвергшихся детскому травматизму, N E , } из которых D E {развилась болезнь и H E H_Eостались здоровыми; и общее число людей, не подвергшихся воздействию, N N , ,}из которых D N D_Nразвилась болезнь и H N }остались здоровыми. Поскольку N E = D E + H E }и аналогично для N N }чисел, у нас есть только четыре независимых числа, которые мы можем организовать в таблицу:
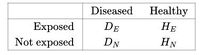
Чтобы избежать возможной путаницы, подчеркнем, что все эти цифры относятся ко всему населению, а не к какой-то его выборке.
Теперь риск развития заболевания при данном воздействии равен D E / N E \(где N E = D E + H E , а при развитии заболевания при отсутствии воздействия- D N / N N . .}это отношение риска, RR, это просто отношение двух,
R R = D E / N E D N / N N ,
который можно переписать как R R = D E N N D N N E = D E / D N N E / N N .
Напротив, шансы заболеть, если подвергнуться D E / H E ,,,}воздействию, против шансов заболеть, если не подвергнуться D N / H N . ,.}воздействию, отношение шансов, или, является отношением двух,
O R = D E / H E D N / H N , } который можно переписать как O R = D E H N D N H E = D E / D N H E / H N .
Мы уже можем отметить, что если заболевание встречается редко, то OR=RR. Действительно, для редкого заболевания мы будем иметь D E ≪ H E , }и так D E + H E ≈ H E ; }, но тогда D E / ( D E + H E ) ≈ D E / H E , }другими словами, для подверженной воздействию популяции риск развития заболевания примерно равен шансам. Аналогичное рассуждение показывает, что риск приблизительно равен шансам для незащищенной популяции, но тогда отношение рисков, которое равно RR, приблизительно равно отношению шансов, которое равно OR. Или мы могли бы просто заметить, что предположение о редком заболевании говорит об этом N E ≈ H E }и N N ≈ H N , ,}из чего следует, что N E / N N ≈ H E / H N , ,} другими словами, знаменатели в конечных выражениях для RR и OR примерно одинаковы. Числители точно такие же, и поэтому мы снова приходим к выводу, что OR ≈ RR. Возвращаясь к нашему гипотетическому исследованию, проблема, с которой мы часто сталкиваемся, заключается в том, что у нас может не быть данных для оценки этих четырех чисел. Например, у нас может не быть общепопуляционных данных о том, кто получил или не получил травму в детстве.
Часто мы можем преодолеть эту проблему, используя случайную выборку из населения: а именно, если ни болезнь, ни воздействия травмы очень редки в наше население, то мы можем выбрать (допустим) сто людей наугад, и выяснить эти четыре числа в выборке; при условии, что выборка репрезентативна достаточно населения, тогда РР, вычисленный для данного образца будет хорошая оценка за рублей для всего населения.
Однако некоторые заболевания могут быть настолько редкими, что, по всей вероятности, даже большая случайная выборка может не содержать даже одного больного индивидуума (или она может содержать несколько, но слишком мало, чтобы быть статистически значимой). Это сделало бы невозможным вычисление RR. Но, тем не менее , мы можем быть в состоянии оценить или, при условии, что, в отличие от болезни, воздействие детской травмы не слишком редко. Конечно, поскольку болезнь встречается редко, это также наша оценка для RR.
Глядя на конечное выражение для OR: дробь в числителе, D E / D N , ,}мы можем оценить, собрав все известные случаи заболевания (предположительно, их должно быть несколько, иначе мы, вероятно, не стали бы проводить исследование в первую очередь), и посмотреть, сколько больных людей подверглось воздействию, а сколько нет. А дробь в знаменателе- H E / H N , ,}это вероятность того, что здоровый индивид в популяции подвергся детскому травматизму. Теперь заметим, что эти последние шансы действительно могут быть оценены путем случайной выборки населения-при условии, как мы уже говорили, что распространенность степень воздействия детской травмы не слишком мала, так что случайная выборка приемлемого размера, скорее всего, будет содержать достаточное количество лиц, подвергшихся воздействию. Так что здесь болезнь встречается очень редко, но фактор, который считается способствующим ей, не так уж и редок; такие ситуации довольно распространены на практике.
Таким образом, мы можем оценить OR, а затем, снова ссылаясь на предположение о редком заболевании, мы говорим, что это также хорошее приближение RR. Кстати, описанный выше сценарий является парадигматическим примером исследования случай-контроль.
Та же история может быть рассказана без упоминания или, например, так: как только мы имеем, что N E ≈ H E \приблизительно H_⋅10{{{1}}} и N N ≈ H N , } тогда мы имеем, что N E / N N ≈ H E / H N . } , следовательно, если, путем случайной выборки, мы сможем оценить H E / H N , {\displaystyle H_{E}/H_{N},} } тогда, на редкое заболевание предположение, что будет хорошая оценка N E / N N , , которая является все, что нам нужно (кроме того D E / D N , } , который мы, вероятно, уже знаете, изучая отдельные случаи заболевания), чтобы вычислить рублей. Однако в литературе принято явно сообщать об ор, а затем утверждать, что RR приблизительно равен ему.
Определение в терминах групповых коэффициентов[править]
Отношение шансов - это отношение шансов события, происходящего в одной группе, к шансам его возникновения в другой группе. Этот термин также используется для обозначения выборочных оценок этого соотношения. Это могут быть мужчины и женщины, экспериментальная группа и контрольная группаили любая другая дихотомическая классификация. Если вероятности события в каждой из групп равны p1 (первая группа) и p2 (вторая группа), то отношение шансов равно:
p 1 / ( 1 − p 1 ) p 2 / ( 1 − p 2 ) = p 1 / q 1 p 2 / q 2 = p 1 q 2 p 2 q 1 ,
где qx = 1-px. Отношение шансов, равное 1, указывает на то, что исследуемое состояние или событие с одинаковой вероятностью произойдет в обеих группах. Коэффициент шансов, превышающий 1, указывает на то, что данное состояние или событие с большей вероятностью произойдет в первой группе. А отношение шансов меньше 1 указывает на то, что данное состояние или событие с меньшей вероятностью произойдет в первой группе. Соотношение шансов должно быть неотрицательным, если оно определено. Он не определен, если p2q1 равно нулю, то есть если p2 равно нулю или q1 равно нулю.
Определение в терминах совместной и условной вероятностей[править]
Отношение шансов также может быть определено в терминах совместного распределения вероятностей двух бинарных случайных величин. Совместное распределение двоичных случайных величин X и Y может быть записано
Y = 1 Y = 0 X = 1 p 11 p 10 X = 0 p 01 p 00 \end{массив}
где p11, p10, p01 и p00-неотрицательные "клеточные вероятности", сумма которых равна единице. Коэффициенты для Y в пределах двух субпопуляций, определенных X = 1 и X = 0, определяются в терминах условных вероятностей, заданных X, т. е.P(Y|X):
Y = 1 Y = 0 X = 1 p 11 p 11 + p 10 p 10 p 11 + p 10 X = 0 p 01 p 01 + p 00 p 00 p 01 + p 00 \end{массив}
Таким образом соотношение шансов равно
p 11 / ( p 11 + p 10 ) p 10 / ( p 11 + p 10 ) / p 01 / ( p 01 + p 00 ) p 00 / ( p 01 + p 00 ) = p 11 p 00 p 10 p 01
Простое выражение справа, приведенное выше, легко запомнить как произведение вероятностей " согласных ячеек "(X = Y), деленное на произведение вероятностей" несогласных ячеек " (X ≠ Y). Однако обратите внимание, что в некоторых приложениях маркировка категорий как ноль и единица произвольна, поэтому в этих приложениях нет ничего особенного в отношении согласующих и диссонирующих значений.
Симметрия[править]
Если бы мы рассчитали отношение шансов на основе условных вероятностей, заданных Y,
Y = 1 Y = 0 X = 1 p 11 p 11 + p 01 p 10 p 10 + p 00 X = 0 p 01 p 11 + p 01 p 00 p 10 + p 00 end{массив}
мы бы получили тот же результат
p 11 / ( p 11 + p 01 ) p 01 / ( p 11 + p 01 ) / p 10 / ( p 10 + p 00 ) p 00 / ( p 10 + p 00 ) = p 11 p 00 p 10 p 01 .
Другие меры размера эффекта для двоичных данных, такие как относительный риск, не обладают этим свойством симметрии.
Отношение к статистической независимости[править]
Если X и Y независимы, то их совместные вероятности можно выразить в терминах их предельных вероятностей px = P(X = 1) и py = P(Y = 1)следующим образом
Y = 1 Y = 0 X = 1 p x p y p x ( 1 − p y ) X = 0 ( 1 − p x ) p y ( 1 − p x ) ( 1 − p y ) end{массив}
В этом случае отношение шансов равно единице, и наоборот, отношение шансов может быть равно единице только в том случае, если совместные вероятности могут быть учтены таким образом. Таким образом, отношение шансов равно единице тогда и только тогда, когда X и Y независимы. Восстановление вероятностей ячеек из соотношения шансов и предельных вероятностей
Отношение шансов является функцией вероятностей ячеек, и наоборот, вероятности ячеек могут быть восстановлены при условии знания отношения шансов и предельных вероятностей P(X = 1) = p11 + p10 и P(Y = 1) = p11 + P01. Если отношение шансов R отличается от 1, то
p 11 = 1 + ( p 1 ⋅ + p ⋅ 1 ) ( R − 1 ) − S 2 ( R − 1 )
где p1• = p11 + p10, p•1 = p11 + p01, и
S = ( 1 + ( p 1 ⋅ + p ⋅ 1 ) ( R − 1 ) ) 2 + 4 R ( 1 − R ) p 1 ⋅ p ⋅ 1 .
В случае , когда R = 1, мы имеем независимость, поэтому p11 = p1•p•1.
Как только мы получим p11, остальные три клеточные вероятности могут быть легко восстановлены из предельных вероятностей.
Пример[править]
Предположим, что в выборке из 100 мужчин 90 пили вино на предыдущей неделе, в то время как в выборке из 80 женщин только 20 пили вино в тот же период. Шансы мужчины, пьющего вино, равны 90 к 10, или 9: 1, в то время как шансы женщины, пьющей вино, только 20 к 60, или 1:3 = 0,33. Таким образом, соотношение шансов составляет 9/0, 33 или 27, что показывает, что мужчины гораздо чаще пьют вино, чем женщины. Детальный расчет таков:
0.9 / 0.1 0.2 / 0.6 = 0.9 × 0.6 0.1 × 0.2 = 0.54 0.02 = 27
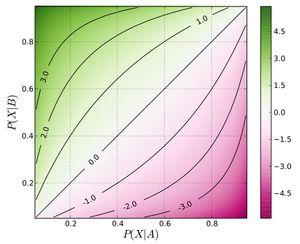
Этот пример также показывает, как коэффициенты шансов иногда чувствительны при определении относительных позиций: в этой выборке мужчины (90/100) / (20/80) = 3,6 раза чаще пьют вино, чем женщины, но имеют в 27 раз больше шансов. Логарифм отношения шансов, разность логитов вероятностей, смягчает этот эффект, а также делает меру симметричной относительно упорядочения групп. Например, используя натуральные логарифмы, отношение шансов 27/1 карт к 3,296 и отношение шансов 1/27 карт к -3,296.
Статистический вывод[править]
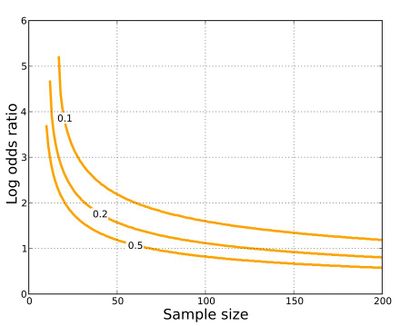
Было разработано несколько подходов к статистическому выводу для коэффициентов шансов.
Один из подходов к выводу использует большие выборочные приближения к выборочному распределению логарифмического отношения шансов (естественный логарифм отношения шансов). Если мы используем общую вероятностную нотацию, определенную выше, отношение шансов журнала населенности равно
log ( p 11 p 00 p 01 p 10 ) = log ( p 11 ) + log ( p 00 ) − log ( p 10 ) − log ( p 01 ) . ,
Если мы наблюдаем данные в виде таблицы непредвиденных обстоятельств
Y = 1 Y = 0 X = 1 n 11 n 10 X = 0 n 01 n 00 \end{массив}
тогда вероятности в совместном распределении можно оценить как
Y = 1 Y = 0 X = 1 p ^ 11 p ^ 10 X = 0 p ^ 01 p ^ 00 end{массив}
где ︿pij = nij / n, причем n = N11 + n10 + n01 + n00 является суммой всех четырех подсчетов ячеек. Коэффициент логарифмических шансов выборки равен
L = log ( p ^ 11 p ^ 00 p ^ 10 p ^ 01 ) = log ( n 11 n 00 n 10 n 01 ) right)}.
Распределение логарифмического отношения шансов примерно нормально с:
L ∼ N ( log ( O R ) , σ 2 ) .
Стандартная ошибка для логарифмического отношения шансов составляет приблизительно
S E = 1 n 11 + 1 n 10 + 1 n 01 + 1 n 00
Это асимптотическое приближение, и оно не даст значимого результата, если любое количество клеток очень мало. Если L-отношение логарифмических шансов выборки, то приблизительный 95% доверительный интервал для отношения логарифмических шансов популяции равен L ± 1,96 SE. Это можно сопоставить с exp(L − 1.96 SE), exp(L + 1.96 SE), чтобы получить 95% доверительный интервал для отношения шансов. Если мы хотим проверить гипотезу о том, что отношение шансов популяции равно единице , то двустороннее p-значение равно 2P(Z < - |L|/SE), где P обозначает вероятность, а Z − стандартную нормальную случайную величину.
Альтернативный подход к умозаключению для коэффициентов шансов рассматривает распределение данных условно на предельных частотах X и Y. Преимущество этого подхода состоит в том, что выборочное распределение отношения шансов может быть выражено точно.
Роль в логистической регрессии[править]
Логистическая регрессия - это один из способов обобщения отношения шансов за пределами двух бинарных переменных. Предположим , что у нас есть двоичная переменная ответа Y и двоичная переменная предиктора X, а также другие переменные предиктора Z1,..., Zp, который может быть двоичным, а может и не быть. Если мы используем множественную логистическую регрессию для регрессии Y на X, Z1, ..., Zp, то расчетный коэффициент β ^ x шляпа {\бета }}_{x}для X связан с условным отношением шансов. В частности, на уровне населения
exp ( β x ) = P ( Y = 1 ∣ X = 1 , Z 1 , … , Z p ) / P ( Y = 0 ∣ X = 1 , Z 1 , … , Z p ) P ( Y = 1 ∣ X = 0 , Z 1 , … , Z p ) / P ( Y = 0 ∣ X = 0 , Z 1 , … , Z p ) ,
такова exp ( β ^ x ) )и оценка этого условного отношения шансов. Интерпретация exp ( β ^ x ) )ИС как оценка отношения шансов между Y и X при значениях Z1, ..., Zp удерживаются фиксированными.
Нечувствительность к типу выборки[править]
Если данные образуют "популяционную выборку", то вероятности ячеек ∧pij интерпретируются как частоты каждой из четырех групп в популяции, определяемые их значениями X и Y. Во многих случаях получение выборки населения нецелесообразно, поэтому используется выбранная выборка. Например, мы можем выбрать выборку единиц с X = 1 с заданной вероятностью f, независимо от их частоты в популяции (что потребует выборки единиц с X = 0 с вероятностью 1 − f). В этой ситуации наши данные будут следовать следующим совместным вероятностям:
Y = 1 Y = 0 X = 1 f p 11 p 11 + p 10 f p 10 p 11 + p 10 X = 0 ( 1 − f ) p 01 p 01 + p 00 ( 1 − f ) p 00 p 01 + p 00 end{массив}
Отношение шансов p11p00 / p01p10 для этого распределения не зависит от величины f. Это показывает, что отношение шансов (и, следовательно, логарифмическое отношение шансов) инвариантно к неслучайной выборке, основанной на одной из исследуемых переменных. Обратите внимание, однако, что Стандартная ошибка логарифмического отношения шансов действительно зависит от значения f.
Этот факт используется в двух важных ситуациях:
- Предположим, что неудобно или непрактично получать выборку населения, но практично получить удобную выборку единиц с различными значениями X, такими, что в пределах x = 0 и X = 1 подвыборок значения Y репрезентативны для населения (т. е. они следуют правильным условным вероятностям).
- Предположим, что предельное распределение одной переменной, скажем X, очень искажено. Например, если мы изучаем связь между высоким потреблением алкоголя и раком поджелудочной железы в общей популяции, частота рака поджелудочной железы будет очень низкой, поэтому потребуется очень большая популяционная выборка, чтобы получить скромное число случаев рака поджелудочной железы. Однако мы могли бы использовать данные больниц, чтобы связаться с большинством или всеми их пациентами с раком поджелудочной железы, а затем случайным образом отобрать равное количество пациентов без рака поджелудочной железы (это называется "исследование случай-контроль").
В обоих этих случаях соотношение шансов может быть рассчитано на основе выбранной выборки без смещения результатов относительно того, что было бы получено для выборки населения.
Использование в количественных исследованиях[править]
В связи с широким использованием логистической регрессии, коэффициент шансов широко используется во многих областях медицинских и социальных исследований. Отношение шансов обычно используется в обзорных исследованиях, в эпидемиологиии для выражения результатов некоторых клинических исследований, таких как исследования случай-контроль. В отчетах оно часто сокращается до "или". Когда данные нескольких обследований объединяются,они часто выражаются как "Объединенные или".
Отношение к относительному риску[править]
В клинических исследованиях, как и в некоторых других условиях, наибольший интерес представляет параметр относительного риска, а не соотношение шансов. Относительный риск лучше всего оценивается с помощью населения образец, но если редкое заболевание предположение держится, отношение шансов является хорошим приближением относительный риск — шансы есть Р / (1 − р), когда р движется в сторону нуля, 1 − п движется к 1, Что означает, что шансы подходы риск и отношение шансов подходы относительного риска.[4] Когда предположение о редком заболевании не выполняется, отношение шансов может завышать относительный риск.
Если абсолютный риск в контрольной группе имеется, то конверсия между ними рассчитывается по формуле:
R R ≈ O R 1 − R C + ( R C × O R )
где:
RR = относительный риск Или = соотношение шансов RC = абсолютный риск в неэкспонированной группе, заданный в виде дроби (например: заполните 10% - ный риск как 0,1)
Заблуждения и преувеличения[править]
В медицинской литературе соотношение шансов часто путают с относительным риском. Для тех, кто не занимается статистикой, соотношение шансов-это трудная для понимания концепция, и она дает более впечатляющую цифру для эффекта. однако большинство авторов считают, что относительный риск легко понять. в одном исследовании члены Национального Фонда борьбы с болезнями фактически в 3,5 раза чаще, чем не члены, слышали о распространенном лечении этой болезни – но соотношение шансов составляло 24, и в статье говорилось, что члены "более чем в 20 раз чаще слышали о" лечении. Исследование статей, опубликованных в двух журналах, показало, что 26% статей, в которых использовался коэффициент шансов, интерпретировали его как коэффициент риска.
Это может отражать простой процесс непонимания авторов, выбирающих наиболее впечатляющую и публикуемую фигуру.Но в некоторых случаях его использование может быть намеренно обманчивым. было высказано предположение, что отношение шансов должно быть представлено только как мера размера эффекта, когда отношение риска не может быть оценено непосредственно.
Обратимость и инвариантность[править]
Отношение шансов имеет еще одно уникальное свойство быть непосредственно математически обратимым, независимо от того, анализируется ли или как выживаемость болезни или частота начала болезни – где или для выживания является прямой обратной величиной 1/или для риска. Это известно как "инвариантность отношения шансов". В отличие от этого, относительный риск не обладает этим математически обратимым свойством при изучении выживаемости болезни в сравнении с частотой возникновения. Это явление обратимости или по сравнению с необратимостью RR лучше всего проиллюстрировать на примере:
Предположим, что в клиническом исследовании риск нежелательных явлений составляет 4/100 в группе лекарств и 2/100 в группе плацебо... это дает RR=2 и OR=2,04166 для неблагоприятного риска по сравнению с плацебо. Однако, если бы анализ был перевернут и неблагоприятные события были вместо этого проанализированы как бессобытийная выживаемость, то группа лекарств имела бы коэффициент 96/100, а группа плацебо имела бы коэффициент 98/100, дающий лекарство против плацебо a RR=0,9796 для выживания, но OR=0,48979. Как видно, RR 0.9796 явно не является обратной величиной RR 2. Напротив, ОР 0,48979 действительно является прямой реципрокностью ОР 2,04166.
Это опять же то, что называется "инвариантностью отношения шансов", и почему RR для выживания не то же самое, что RR для риска, в то время как OR имеет это симметричное свойство при анализе либо выживания, либо неблагоприятного риска. Опасность для клинической интерпретации ОР возникает тогда, когда частота нежелательных явлений не является редкой, тем самым преувеличивая различия, когда предположение о редком заболевании не выполняется. С другой стороны, когда болезнь встречается редко, использование RR для выживания (например RR=0,9796 из приведенного выше примера) может клинически скрывать и скрывать важное удвоение неблагоприятного риска, связанного с лекарством или воздействием.
Оценщики отношения шансов[править]
Примерное соотношение шансов[править]
Соотношение шансов выборки n11n00 / n10n01 легко вычисляется, и для умеренных и больших выборок хорошо работает в качестве оценщика отношения шансов популяции. Когда одна или несколько ячеек в таблице непредвиденных обстоятельств могут иметь небольшое значение, отношение шансов выборки может быть смещено и демонстрировать высокую дисперсию.
Альтернативные оценки[править]
Был предложен ряд альтернативных оценок отношения шансов для устранения ограничений выборочного отношения шансов. Одной из альтернативных оценок является условная оценка максимального правдоподобия, которая обусловливает поля строк и столбцов при формировании вероятности максимизации (как в точном тесте Фишера). другой альтернативной оценкой является оценка Мантеля–Хенцеля.
Численные примеры[править]
Следующие четыре таблицы непредвиденных обстоятельств содержат количество наблюдаемых ячеек, а также соответствующее отношение шансов выборки (OR) и отношение логарифмических шансов выборки (LOR):
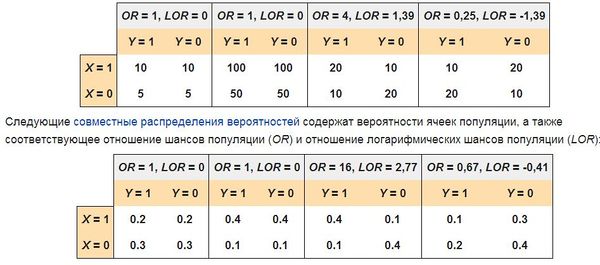
Численный пример[править]
Пример снижения риска
| Экспериментальная группа (Е) | Контрольная группа (с) | Весь | |
|---|---|---|---|
| События (E) | EE = 15 | CE = 100 | 115 |
| Не-события (N) | EN = 135 | CN = 150 | 285 |
| Всего предметов (ов) | ES = EE + EN = 150 | CS = CE + CN = 250 | 400 |
| Частота событий (ER) | EER = EE / ES = 0,1, или 10% | CER = CE / CS = 0,4, или 40% |
| Уравнение | Переменная | Сокр. | Ценность |
|---|---|---|---|
| CER-EER | абсолютное снижение риска | ПРИБЫТИЕ | 0,3, или 30% |
| (CER - EER) / CER | относительное снижение риска | РРР | 0,75, или 75% |
| 1 / (CER − EER) | количество, необходимое для лечения | NNT | 3.33 |
| EER / CER | коэффициент риска | Р-Р | 0.25 |
| (EE / EN) / (CE / CN) | отношение шансов | ИЛИ | 0.167 |
| (CER - EER) / CER | предотвратимая фракция среди неэкспонированных | PFu | 0.75 |
Связанная статистика[править]
См. также: категория: Сводная статистика для таблиц непредвиденныхобстоятельств .
Существуют различные другие сводные статистические данные для таблиц непредвиденных обстоятельств, которые измеряют связь между двумя событиями , такими как Y Юла, QЮла ; эти два нормализованы таким образом, что они равны 0 для независимых событий, 1 Для идеально коррелированных, -1 для идеально отрицательно коррелированных. Эдвардс (1963) изучил их и доказал, что эти меры ассоциации должны быть функциями отношения шансов, которое он назвал перекрестным отношением.
См. также[править]
- Ч Коэна
- Кросс-коэффициент
- Диагностическое отношение шансов
- Лесной участок
- Коэффициент опасности
- Отношение правдоподобия
- Коэффициент скорости
Источники[править]
- Edwards, A. W. F. (1963). "Мера ассоциации в таблице 2 × 2". Журнал Королевского статистического общества. генерал).