Теорема о раскраске дорог

В теории графов теорема о раскраске дорог, известная до недавнего времени как гипотеза о раскраске дорог, имеет дело с синхронизированными инструкциями. Вопрос заключается в том, можно ли с помощью таких инструкций достичь или найти объект или пункт назначения из любой другой точки сети (которая может быть представлением городских улиц или лабиринта).[1] в реальном мире это было бы так, как если бы вы позвонили другу, чтобы спросить дорогу к его дому, и он дал вам набор направлений, которые работали независимо от того, откуда вы начали. Эта теорема также имеет значение в символической динамике.

Теорема была впервые предложена Роем Адлером и Бенджамином Вайсом (1970). Это было доказано Авраамом Трахтманом (2009).

Направленный граф с синхронизирующей раскраской

Пример и интуиция

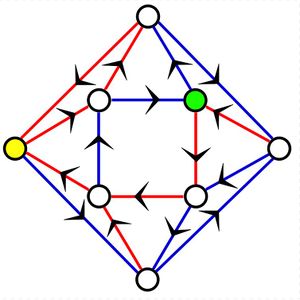
Изображение справа показывает направленный граф на восьми вершинах, в которых каждая вершина имеет степень out-2. (Каждая вершина в этом случае также имеет степень 2, но это не обязательно для существования синхронизирующей раскраски.) Края этого графика были окрашены в красный и синий цвета, чтобы создать синхронизирующую раскраску.

Например, рассмотрим вершину, отмеченную желтым цветом. Независимо от того, где в графике вы начинаете, если вы пересекаете все девять ребер в прогулке "синий-красный-красный—синий-красный-красный—синий-красный-красный", вы окажетесь в желтой вершине. Точно так же, если вы пересекаете все девять ребер в прогулке "синий-синий-красный—синий-синий-красный—синий-синий-красный", вы всегда окажетесь в вершине, отмеченной зеленым цветом, независимо от того, где вы начали.

Теорема о раскраске дорог утверждает, что для определенной категории направленных графов всегда можно создать такую раскраску.

Математическое описание

Пусть G-конечный, сильно связный, направленный граф, где все вершины имеют одинаковую степень выхода k. Пусть a-алфавит, содержащий буквы 1, ..., к. А синхронизация раскраски (также известный как разборная раскраска) В Г - это маркировка краев В Г с букв от А , такие, что

(1) каждая вершина имеет ровно одно исходящее ребро с данной меткой и

(2) для каждой вершины в в графе существует слово ж за собой такого, что все пути в г , соответствующее Вт прекратить на Вольт.

Терминологическая синхронизирующая окраска обусловлена отношением между этим понятием и синхронизирующим словом в теории конечных автоматов.

Чтобы такая окраска вообще существовала, необходимо, чтобы G был апериодическим. теорема о раскраске дорог утверждает, что апериодичность также достаточна для существования такой раскраски. Поэтому проблему окраски дорог можно кратко сформулировать следующим образом:

• Каждый конечный сильно связный направленный апериодический граф равномерной степени выхода имеет синхронизирующую раскраску.

Предыдущие частичные результаты

Предыдущие частичные или специальные результаты включают следующее:

• Если G-конечный сильно связный апериодический направленный граф без множественных ребер, а G содержит простой цикл простой длины, который является собственным подмножеством G, то G имеет синхронизирующую раскраску. (О'Брайен 1981)
• Если G-конечный сильно связный апериодический направленный граф (допускается несколько ребер), и каждая вершина имеет одинаковую степень входа и выхода k, то G имеет синхронизирующую раскраску. (Кари 2003)

См. также

• Теорема о четырех цветах
• Раскраска графика

Читать

• Adler, R. L.; Weiss, B. (1970), подобие автоморфизмов Тора, Memoires of the American Mathematical Society, 98.
• Hegde, Rajneesh; Jain, Kamal (2005)," a min-max теорема о гипотезе окраски дороги", Proc. EuroComb 2005 (PDF), Дискретная математика и теоретическая информатика, стр.
• Kari, Jarkko (2003), "синхронизация конечных автоматов на Эйлеровых орграфах", теоретическая информатика,
• O'Brien, G. L. (1981), "the road-Coloring problem", Israel Journal of Mathematics,
• Trahtman, Avraham N. (2009), "the road coloring problem", Israel Journal of Mathematics,