Теория информации

Материал из wikixw
Перейти к навигации Перейти к поиску

Не путать с информатикой .

Теория информации изучает количественную оценку , хранение и передачу информации . Первоначально Клод Шеннон предложил в 1948 году найти фундаментальные ограничения на обработку сигналов и коммуникационные операции , такие как сжатие данных, в знаковой статье под названием " математическая теория связи ". Его влияние имело решающее значение для успеха миссий Voyager в глубокий космос, изобретения компакт-диска, возможности мобильных телефонов , развития Интернета , изучения лингвистики и человеческого восприятия, понимания черных дыр и множество других полей.

Эта область находится на пересечении математики, статистики, информатики, физики, нейробиологии , информационной инженерии и электротехники . Теория также нашла применение и в других областях, в том числе статистического вывода, обработки естественного языка, криптография, нейробиологии, человеческого зрения, Эволюция и функции молекулярно-коды (биоинформатика), модель выбора в статистике, теплофизика, квантовые вычисления, лингвистики, обнаружения плагиата, распознаванияи обнаружения аномалий. важные подполя теории информации включают в себя: исходное кодирование, канальное кодирование, алгоритмическая теория сложности, алгоритмическая теория информации , Информационно-теоретическая безопасность, теория серых систем и меры информатизации.

Приложения фундаментальных разделов теории информации включают сжатие данных без потерь (например, ZIP-файлы), сжатие данных с потерями (например, MP3s и JPEG) и канальное кодирование (например, для DSL ). Теория информации используется в информационном поиске , сборе разведданных , азартных играх , статистике и даже в музыкальной композиции .

Ключевой мерой в теории информации является "энтропия". Энтропия количественно определяет величину неопределенности, связанной со значением случайной величины или результатом случайного процесса . Например, определение результата справедливого подбрасывания монеты (с двумя равновероятными исходами) дает меньше информации (более низкая энтропия), чем определение результата от броска кубика (с шестью равновероятными исходами). Некоторые другие важные меры в теории информации-это взаимная информация , пропускная способность канала , показатели ошибок и относительная энтропия .

Обзор[править]

Теория информации изучает передачу, обработку, извлечение и использование информации. Абстрактно говоря, информацию можно рассматривать как разрешение неопределенности. В случае передачи информации по зашумленному каналу эта абстрактная концепция была конкретизирована в 1948 году Клодом Шенноном в его работе " математическая теория связи", в котором "информация" мыслится как набор возможных сообщений, где цель состоит в том, чтобы отправить эти сообщения по зашумленному каналу, а затем заставить приемник реконструировать сообщение с низкой вероятностью ошибки, несмотря на шум канала. Основной результат Шеннона-теорема о кодировании по зашумленному каналу-показал, что в пределе использования многих каналов асимптотически достижимая скорость передачи информации равна пропускной способности канала , величина, зависящая только от статистики канала, по которому передаются сообщения.

Теория информации тесно связана с семейством теоретической и прикладной дисциплины, которые были изучены и сводятся к инженерной практике при различных рубрик по всему миру за последние полвека или более: адаптивные системы, упреждающей системы, искусственный интеллект, комплексные системы, сложность науки, кибернетики, информатики, машинного обучения, наряду с системами наук многих описаний. Теория информации-это широкая и глубокая математическая теория, имеющая столь же широкие и глубокие приложения, среди которых важнейшее место занимает теория кодирования .

Теория кодирования занимается поиском явных методов, называемых кодами, для повышения эффективности и снижения частоты ошибок передачи данных по зашумленным каналам до уровня, близкого к пропускной способности канала . Эти коды можно условно разделить на методы сжатия данных (кодирование источника) и исправления ошибок (кодирование канала). В последнем случае потребовалось много лет, чтобы найти методы, доказавшие возможность работы Шеннона.

Третий класс кодов теории информации - это криптографические алгоритмы (как коды, так и шифры ). Понятия, методы и результаты теории кодирования и теории информации широко используются в криптографии и криптоанализе . Смотрите статью запрет (единица измерения) для исторического применения.

Исторический фон[править]

Основная статья: История теории информации

Знаковым событием, которое установило дисциплину теории информации и привлекло к ней пристальное внимание всего мира, стала публикация классической статьи Клода Э. Шеннона "математическая теория коммуникации" в техническом журнале Bell System в июле и октябре 1948 года.

До этой статьи в Bell Labs были разработаны ограниченные теоретико-информационные идеи, все они неявно предполагали события с равной вероятностью. Гарри Найквистас 1924 бумаги, определенные факторы, влияющие на скорость Телеграф, содержит теоретический раздел количественного определения "интеллект" и "скорость линии", по которым оно может быть передано системы коммуникаций, дающие соотношения ж = к журналу м (ссылаясь Больцмана постоянная), где ж - скорость передачи разведданных, м - это количество различных уровней напряжения, чтобы выбрать из на каждом временном шаге, и К является константой. Статья Ральфа Хартли 1928 года, При передаче информации используется слово информация как измеряемая величина, отражающая способность получателя отличать одну последовательность символов от любой другой, что позволяет количественно определить информацию как H = log S n = n log S , где S-число возможных символов, а n-число символов в передаче. Таким образом , единицей информации была десятичная цифра, которую с тех пор иногда называли Хартли в его честь как единицу, шкалу или меру информации. Алан Тьюринг в 1940 году подобные идеи использовались в рамках статистического анализа взлома немецкими шифрами Энигмы Второй мировой войны.

Большая часть математики, стоящей за теорией информации с событиями различной вероятности, была разработана для области термодинамики Людвигом Больцманом и Дж .Виллардом Гиббсом. Связи между теоретико-информационной энтропией и термодинамической энтропией, включая важный вклад Рольфа Ландауэра в 1960-е годы, исследуются в энтропии в термодинамике и теории информации .

В революционной и новаторской статье Шеннона, работа над которой была существенно завершена в Лаборатории Белла к концу 1944 года, Шеннон впервые представил качественную и количественную модель коммуникации как статистический процесс, лежащий в основе теории информации, открываясь утверждением, что 

   "Фундаментальная проблема коммуникации состоит в том, чтобы воспроизвести в одной точке, точно или приблизительно, сообщение, выбранное в другой точке."

Вместе с ним пришли идеи о том, что

  • информационная энтропия и избыточность источника, а также его релевантность через теорему кодирования источника;
  • взаимная информация и пропускная способность канала зашумленного канала, включая обещание идеальной связи без потерь, заданной теоремой о кодировании зашумленного канала;
  • практический результат закона Шеннона-Хартли для пропускной способности канала гауссовского канала ; а также
  • бит-это новый способ видения самой фундаментальной единицы информации.

Количество информации[править]

Основная статья: Количество информации

Теория информации основана на теории вероятностей и статистике . Теория информации часто занимается измерениями информации распределений, связанных со случайными величинами. Важными количествами информации являются энтропия, мера информации в одной случайной переменной , и взаимная информация, мера информации, общей для двух случайных величин. Первая величина является свойством вероятностного распределения случайной величины и дает предел скорости, при которой данные, полученные независимыми выборками с заданным распределением, могут быть достоверно сжал . Последний является свойством совместного распределения двух случайных величин и представляет собой максимальную скорость надежной связи по зашумленному каналу в пределе длинных длин блоков, когда статистика канала определяется совместным распределением.

Выбор логарифмической базы в следующих формулах определяет ту единицу информационной энтропии, которая используется. Общей единицей информации является бит, основанный на двоичном логарифме . Другие единицы измерения включают nat, который основан на натуральном логарифме , и десятичную цифру , которая основана на общем логарифме .

В дальнейшем выражение вида P log p считается по условию равным нулю всякий раз, когда p = 0 . Это оправдано, потому lim p → 0 + p log ⁡ p = 0 =0что для любой логарифмической базы.

Энтропия источника информации[править]

На основе вероятностной массовой функции каждого исходного символа, подлежащего передаче, энтропия Шеннона H, выраженная в единицах бит (на символ), задается следующим образом:

  • H = − ∑ i p i log 2 ⁡ ( p i )

где p i-вероятность появления i-го возможного значения исходного символа. Это уравнение дает энтропию в единицах " бит "(на символ), потому что оно использует логарифм базы 2, и эта мера энтропии базы-2 иногда называлась "Шеннон" в его честь. Энтропия также обычно вычисляется с использованием натурального логарифма (основание e, где e-число Эйлера), которое производит измерение энтропии в " nats"за символ и иногда упрощает анализ, избегая необходимости включать дополнительные константы в формулы. Другие основания также возможны, но менее обыкновенно используемые. Например, логарифм основания 2 8 = 256 будет производить измерение в байтах на символ, а логарифм основания 10 будет производить измерение в десятичных цифрах (или Хартли) на символ.

Интуитивно, энтропия H X дискретной случайной величины X является мерой величины неопределенности, связанной со значением X, когда известно только его распределение.

Энтропия источника, который испускает последовательность из N символов, которые являются независимыми и одинаково распределенными (iid), составляет N ⋅ H бит (на сообщение из N символов). Если исходные символы данных распределены одинаково, но не являются независимыми, то энтропия сообщения длины N будет меньше, чем N ⋅ H .

Энтропия проб Бернулли как функция вероятности успеха, часто называемая двоичной функцией энтропии, H b (p ) . Энтропия максимизируется на 1 бит за испытание, когда два возможных результата являются одинаково вероятными, как и при непредвзятом подбрасывании монеты.

Если один передает 1000 бит (0s и 1s), и значение каждого из этих битов известно получателю (имеет определенное значение с уверенностью) перед передачей, ясно, что никакая информация не передается. Если, однако, каждый бит независимо с одинаковой вероятностью будет равен 0 или 1, то было передано 1000 шэннонов информации (чаще называемых битами). Между этими двумя крайностями информация может быть количественно выражена следующим образом. Если 𝕏 - это множество всех сообщений { x 1,..., x n } , что X может быть, и p (x) - вероятность некоторого x ∈ X , то энтропия, H, X определяется:

  • H ( X ) = E X [ I ( x ) ] = − ∑ x ∈ X p ( x ) log ⁡ p ( x ) .

(Здесь I (x)-это самоинформация , которая является вкладом энтропии отдельного сообщения, а 𝔼 X-ожидаемое значение .) Свойство энтропии заключается в том, что она максимизируется, когда все сообщения в пространстве сообщений равнопробируемы p ( x ) = 1/ n ; т. е. наиболее непредсказуемы, и в этом случае H ( X ) = log n .

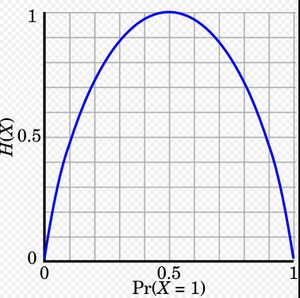
Частным случаем информационной энтропии для случайной величины с двумя исходами является двоичная функция энтропии, обычно принимаемая за логарифмическое основание 2, таким образом, имеющее единицу Шеннона (Sh) :

  • H b ( p ) = − p log 2 ⁡ p − ( 1 − p ) log 2 ⁡ ( 1 − p ) . .

Совместная энтропия[править]

Совместная энтропия двух дискретных случайных величин X и Y-это просто энтропия их спаривания: ( X , Y ) . Это означает , что если X и Y независимы, то их совместная энтропия является суммой их индивидуальных энтропий.

Например , если ( X, Y ) представляет положение шахматной фигуры — X строка и Y столбец, то совместная энтропия строки фигуры и столбца фигуры будет энтропией положения фигуры.

  • H ( X , Y ) = E X , Y [ − log ⁡ p ( x , y ) ] = − ∑ x , y p ( x , y ) log ⁡ p ( x , y )

Несмотря на сходные обозначения, совместную энтропию не следует путать с перекрестной энтропией .

Условная энтропия (эквивокация)[править]

Условная энтропия или условная неопределенность X заданной случайной величины Y (также называемая эквивокацией X относительно Y ) является средней условной энтропией по Y :

  • H ( X | Y ) = E Y [ H ( X | y ) ] = − ∑ y ∈ Y p ( y ) ∑ x ∈ X p ( x | y ) log ⁡ p ( x | y ) = − ∑ x , y p ( x , y ) log ⁡ p ( x | y ) .

Поскольку энтропия может быть обусловлена случайной величиной или тем, что эта случайная величина является определенной величиной, следует позаботиться о том, чтобы не путать эти два определения условной энтропии, первое из которых является более распространенным. Основное свойство этой формы условной энтропии заключается в том, что:

  • H ( X | Y ) = H ( X , Y ) − H ( Y ) .

Взаимная информация (transinformation)[править]

Взаимная информация измеряет количество информации,которую можно получить об одной случайной величине, наблюдая за другой. Это важно в общении, где он может быть использован для максимального количества информации, разделяемой между отправленными и полученными сигналами. Взаимная информация X относительно Y задается с помощью:

  • I ( X ; Y ) = E X , Y [ S I ( x , y ) ] = ∑ x , y p ( x , y ) log ⁡ p ( x , y ) p ( x ) p ( y )

где SI (s специфическая взаимная информация) - это точечная взаимная информация .

Основным свойством взаимной информации является то, что

  • I ( X ; Y ) = H ( X ) − H ( X | Y ) .

То есть , зная Y, мы можем сохранить среднее значение i ( X ; Y ) битов в кодировке X по сравнению с незнанием Y .

Взаимная информация симметрична:

  • I ( X ; Y ) = I ( Y ; X ) = H ( X ) + H ( Y ) − H ( X , Y ) .

Взаимная информация может быть выражена как среднее расхождение Kullback–Leibler (информационный выигрыш) между апостериорным распределением вероятностей X, заданным значением Y, и предшествующим распределением на X:

  • I ( X ; Y ) = E p ( y ) [ D K L ( p ( X | Y = y ) ‖ p ( X ) ) ] .

Другими словами, это мера того, насколько в среднем изменится распределение вероятности по X, если нам будет дано значение Y . Это часто пересчитывается как отклонение от произведения предельных распределений на фактическое совместное распределение:

  • I ( X ; Y ) = D K L ( p ( X , Y ) ‖ p ( X ) p ( Y ) ) .

Взаимная информация тесно связана с тестом логарифмического отношения правдоподобия в контексте таблиц сопряженности и полиномиального распределения и с тестом Pear 2 Пирсона: взаимная информация может рассматриваться как статистика для оценки независимости между парой переменных и имеет четко определенное асимптотическое распределение.

Kullback-leibler дивергенция (увеличение информации)[править]

Дивергенция Кульбака-Лейблера(или информационная дивергенция , информационный выигрыш или относительная энтропия) - это способ сравнения двух распределений: "истинного" распределения вероятностей p(X) и произвольного распределения вероятностей q (X) . Если мы сжимаем данные таким образом, что предполагается, что q(X) является распределением, лежащим в основе некоторых данных, когда на самом деле p(X) является правильным распределением, расхождение Kullback–Leibler-это число средних дополнительных битов на датум, необходимых для сжатия. Это так определено

  • D K L ( p ( X ) ‖ q ( X ) ) = ∑ x ∈ X − p ( x ) log ⁡ q ( x ) − ∑ x ∈ X − p ( x ) log ⁡ p ( x ) = ∑ x ∈ X p ( x ) log ⁡ p ( x ) q ( x ) .

Хотя он иногда используется в качестве "метрики расстояния", дивергенция KL не является истинной метрикой, поскольку она не симметрична и не удовлетворяет неравенству треугольника (что делает его полу-квазиметрическим).

Другая интерпретация расхождения KL - это "ненужная неожиданность", введенная априором от истины: предположим, что число X собирается быть случайным образом извлечено из дискретного множества с распределением вероятностей p(x) . Если Алиса знает истинное распределение p (x) , в то время как Боб считает(имеет априор), что распределение является q (x), то Боб будет более удивлен, чем Алиса, в среднем, увидев значение X . Расхождение KL - это (объективное) ожидаемое значение неожиданности Боба (субъективной) минус неожиданность Алисы, измеренная в битах, если лог находится в базе 2. Таким образом, степень, в которой Приор боба является "неправильным", может быть количественно оценена с точки зрения того, насколько "неоправданно удивленным" он, как ожидается, сделает его.

Другие количества[править]

Другие важные теоретико-информационные величины включают релевантную энтропию (обобщение энтропии), дифференциальную энтропию (обобщение количеств информации на непрерывные распределения) и условную взаимную информацию .

Теория кодирования[править]

Основная статья: Теория кодирования

Изображение, показывающее царапины на читаемой поверхности CD-R. музыка и компакт-диски с данными кодируются с помощью кодов исправления ошибок и, таким образом, все еще могут быть прочитаны, даже если они имеют незначительные царапины с помощью обнаружения и исправления ошибок

Теория кодирования является одним из наиболее важных и непосредственных приложений теории информации. Его можно подразделить на теорию кодирования источника и теорию кодирования канала. Используя статистическое описание данных, теория информации количественно определяет количество битов, необходимых для описания данных, которое является информационной энтропией источника.

  • Сжатие данных (исходное кодирование): существует две формулировки для задачи сжатия:
  • сжатие данных без потерь : данные должны быть восстановлены точно;
  • сжатие данных с потерями: выделение битов, необходимых для восстановления данных, в пределах заданного уровня точности, измеряемого функцией искажения. Это подмножество теории информации называется теорией скоростных искажений .
  • Коды с исправлением ошибок( канальное кодирование): в то время как сжатие данных удаляет как можно больше избыточности, код с исправлением ошибок добавляет Только правильный вид избыточности (т. е. исправление ошибок), необходимый для эффективной и точной передачи данных по зашумленному каналу.

Это разделение теории кодирования на сжатие и передачу обосновывается теоремами передачи информации, или теоремами разделения источника и канала, которые оправдывают использование битов в качестве универсальной валюты для информации во многих контекстах. Однако эти теоремы справедливы только в том случае, когда один передающий пользователь желает связаться с одним принимающим пользователем. В сценариях с более чем одним передатчиком (канал множественного доступа), более чем одним приемником (широковещательный канал) или промежуточными "помощниками" (ретрансляционный канал) или более общими сетями, сжатие с последующей передачей может больше не быть оптимальным. Теория сетевой информации относится к этим мультиагентным моделям коммуникации.

Теория источников[править]

Любой процесс, который генерирует последовательные сообщения, может рассматриваться как источник информации. Источник без памяти-Это такой источник , в котором каждое сообщение является независимой одинаково распределенной случайной величиной, тогда как свойства эргодичности и стационарности накладывают менее ограничительные ограничения. Все такие источники являются стохастическими . Эти термины хорошо изучены сами по себе вне теории информации.

Оценка[править]

Скорость передачи информации - это средняя энтропия на символ. Для источников без памяти это просто энтропия каждого символа, в то время как в случае стационарного стохастического процесса она равна

  • r = lim n → ∞ H ( X n | X n − 1 , X n − 2 , X n − 3 , … ) ;

то есть условная энтропия символа задается всеми предыдущими сгенерированными символами. Для более общего случая процесса, который не обязательно является стационарным, средняя скорость равна

  • r = lim n → ∞ 1 n H ( X 1 , X 2 , … X n ) ;

то есть предел совместной энтропии на символ. Для стационарных источников эти два выражения дают один и тот же результат.

В теории информации принято говорить о" скорости "или" энтропии " языка. Это уместно, например, когда источником информации является английская проза. Скорость источника информации связана с его избыточностью и тем , насколько хорошо он может быть сжат, предметом исходного кодирования .

Емкость канала[править]

Основная статья: Емкость канала

Коммуникации по каналу—например , кабель ethernet-это основная мотивация теории информации. Однако, как известно любому, кто когда-либо использовал телефон (мобильный или стационарный), такие каналы часто не дают точной реконструкции сигнала; шум, периоды тишины и другие формы повреждения сигнала часто ухудшают качество.

Рассмотрим процесс связи по дискретному каналу. Простая модель процесса показана ниже:

описание

Здесь X представляет собой пространство передаваемых сообщений, а Y-пространство сообщений, полученных в течение единичного времени по нашему каналу. Пусть p (y | x) - условная функция распределения вероятностей Y по заданному X . Мы будем считать, что p (y | x ) является неотъемлемым фиксированным свойством нашего канала связи (представляющим природу шума нашего канала). Тогда совместное распределение X и Y полностью определяется нашим каналом и нашим выбором f ( x), предельное распределение сообщений, которые мы выбираем для отправки по каналу. При таких ограничениях мы хотели бы максимально увеличить скорость передачи информации,или сигнала, который мы можем передавать по каналу. Подходящей мерой для этого является взаимная информация , и эта максимальная взаимная информация называется пропускной способностью канала и задается путем:

  • C = max f I ( X ; Y ) . \!

Эта емкость имеет следующее свойство, связанное со скоростью передачи информации R (где R обычно представляет собой бит на символ). Для любой скорости передачи информации R < C и ошибки кодирования ε > 0, для достаточно больших > N существует код длины N и скорости ≥ R и алгоритм декодирования, такой, что максимальная вероятность ошибки блока составляет ≤ ε; то есть всегда можно передавать с произвольно малой ошибкой блока. Кроме того , для любой скорости R > C>, невозможно передать с произвольно малой ошибкой блока.

Канальное кодирование связано с поиском таких почти оптимальных кодов, которые могут быть использованы для передачи данных по зашумленному каналу с небольшой ошибкой кодирования со скоростью, близкой к пропускной способности канала.

Емкость конкретных моделей каналов[править]

описание
  • Непрерывный аналоговый канал связи с учетом гауссовского шума-см. теорему Шеннона-Хартли .
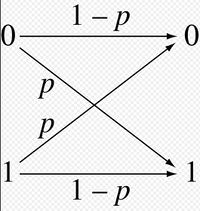
  • Двоичный симметричный канал (BSC) с вероятностью кроссовера p является двоичным входом, двоичным выходным каналом, который переворачивает входной бит с вероятностью p . BSC имеет емкость битов 1-H b (p ) в пользу канала, где H b бинарная функция энтропии к логарифму основания-2:


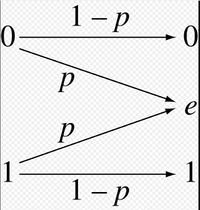
  • Двоичный канал стирания (BEC) с вероятностью стирания p является двоичным входом, троичным выходным каналом. Возможные выходные сигналы канала-0, 1 и третий символ 'e', называемый стиранием. Стирание представляет собой полную потерю информации о входном бите. Емкость BEC составляет 1-p бит на использование канала.
описание

Приложения к другим полям[править]

Использование разведки и приложений секретности[править]

Теоретико-информационные концепции применимы к криптографии и криптоанализу . Информационный блок Тьюринга, the ban, был использован в проекте Ultra, взломав немецкий машинный код Enigma и ускорив окончание Второй мировой войны в Европе . Шеннон сам определил важное понятие, которое теперь называется расстоянием уникальности . Основываясь на избыточности открытого текста , он пытается дать минимальный объем зашифрованного текста, необходимый для обеспечения уникальной дешифруемости.

Теория информации приводит нас к убеждению, что хранить секреты гораздо труднее, чем может показаться на первый взгляд. Атака грубой силы может разрушить системы, основанные на алгоритмах асимметричного ключа или на наиболее часто используемых методах алгоритмов симметричного ключа (иногда называемых алгоритмами секретного ключа), таких как блочные шифры . Безопасность всех таких методов в настоящее время исходит из предположения, что никакая известная атака не может сломать их в практическом количестве времени.

Информационная теоретическая безопасность относится к таким методам, как одноразовая pad, которые не являются уязвимыми для таких атак грубой силы. В таких случаях положительная условная взаимная информация между открытым текстом и шифртекстом (обусловленная ключом) может обеспечить надлежащую передачу, в то время как безусловная взаимная информация между открытым текстом и шифрованным текстом остается нулевой, что приводит к абсолютно безопасным коммуникациям. Другими словами, подслушивающий не сможет улучшить свою догадку об открытом тексте, получив знания о шифртексте, но не о ключе. Однако, как и в любой другой криптографической системе, необходимо проявлять осторожность, чтобы правильно применять даже теоретически безопасные методы защиты информации; проект Venona смог взломать одноразовые колодки Советского Союза из-за их неправильного повторного использования ключевого материала.

Генерация псевдослучайных чисел[править]

Генераторы псевдослучайных чисел широко доступны в библиотеках компьютерных языков и прикладных программах. Они, почти повсеместно, непригодны для криптографического использования, поскольку они не уклоняются от детерминированной природы современного компьютерного оборудования и программного обеспечения. Класс улучшенных генераторов случайных чисел называется криптографически защищенными генераторами псевдослучайных чисел, но даже они требуют, чтобы случайные семена, внешние по отношению к программному обеспечению, работали по назначению. Эти можно получить через экстракторы, если сделано тщательно. Мерой достаточной случайности в экстракторах является мин-энтропия, значение, связанное с энтропией Шеннона через Rényi entropy; rényi entropy также используется для оценки случайности в криптографических системах. Хотя и связанные, различия между этими мерами означают, что случайная величина с высокой энтропией Шеннона не обязательно удовлетворительна для использования в экстракторе и поэтому для использования в криптографии.

Сейсмическая разведка[править]

Одно из первых коммерческих применений теории информации было в области сейсмической разведки нефти. Работа в этой области позволила снять и отделить нежелательный шум от нужного сейсмического сигнала. Теория информации и цифровая обработка сигналов предлагают значительное улучшение разрешения и четкости изображения по сравнению с предыдущими аналоговыми методами.

Семиотика[править]

Семиотики Doede Nauta и Winfried Nöth оба рассматривали Чарльза Сандерса пирса как создавшего теорию информации в своих работах по семиотике. Наута определил семиотическую теорию информации как изучение " внутренних процессов кодирования, фильтрации и обработки информации."[13]:91

Понятия теории информации, такие как избыточность и код контроля были использованы семиотистов, таких как Умберто Эко и Ферруччо Росси-Ланди , чтобы объяснить идеологию как форму передачи сообщений, при которой господствующий социальный класс возводит его в сообщение с помощью знаков, которые обладают высокой степенью избыточности такого, что только одно сообщение декодируется среди множества конкурентов.

Различные приложения[править]

Теория информации также находит применение в азартных играх и инвестициях , черных дырах и биоинформатике .

Смотрите также[править]

Приложения

История

Теория

Понятия

Пруф[править]

.encyclopediaofmath.org/index.php/Information

Источник — https://wikixw.ru/index.php?title=Теория_информации&oldid=9490