Теория узлов

В топологии теория узла-исследование математических узлов . В то время как вдохновленный узлами, которые появляются в повседневной жизни, такими как шнурки и веревка, математический узел отличается тем, что концы соединены вместе, так что он не может быть отменен, самый простой узел является кольцом (или "неизвестным") . В математическом языке узел-вложение круга в 3-мерное Евклидово пространство, R 3 (в топологии круг не связан с классическим геометрическим понятием, но со всеми его гомеоморфизмами ). Два математических узла эквивалентны, если один может быть преобразован в другой через деформацию R3 на себя (известный как окружающая изотопия ); эти преобразования соответствуют манипуляциям завязанной последовательности, которые не вовлекают сокращение последовательности или передачу последовательности через себя.
Узлы могут быть описаны различными способами. Однако, учитывая метод описания, может быть более одного описания, которое представляет один и тот же узел. Например, распространенным методом описания узла является плоская диаграмма, называемая диаграммой узлов. Любой данный узел может быть нарисован различными способами, используя диаграмму узлов. Поэтому фундаментальной проблемой в теории узлов является определение, когда два описания представляют один и тот же узел.

Существует полное алгоритмическое решение этой проблемы, которое имеет неизвестную сложность . На практике узлы часто различаются с помощью инварианта узла, "количества", которое является одинаковым при вычислении из разных описаний узла. Важные инварианты включают многочлены узлов , группы узлов и гиперболические инварианты.
Первоначальная мотивация для основателей теории узлов заключалась в создании таблицы узлов и связей , которые представляют собой узлы из нескольких компонентов, запутанных друг с другом. Более шести миллиардов узлов и связей были сведены в таблицу с начала теории узлов в 19 веке.
Чтобы получить дальнейшее представление, математики обобщили понятие узла несколькими способами. Узлы могут быть рассмотрены в других трехмерных пространствах, и могут быть использованы объекты, отличные от кругов; см. узел (математика) . Многомерные узлы - это N-мерные сферы в m-мерном Евклидовом пространстве.
История[править]
Основная статья: История теории узлов
Археологи обнаружили, что завязывание узлов восходит к доисторическим временам. Помимо их использования, таких как запись информации и связывание объектов вместе, узлы заинтересовали людей своей эстетикой и духовной символикой. Узлы появляются в различных формах китайского художественного произведения датируя от нескольких столетий BC (см. китайский завязывать). Бесконечный узел появляется в тибетском буддизме, в то время как Борромейские кольца неоднократно появлялись в разных культурах, часто представляя силу в единстве. Кельтские монахи, создавшие Келлскую Книгу, щедро осыпали целые страницы замысловатыми текстами. Кельтский узелок .
Математическая теория узлов была впервые разработана в 1771 году Александром-Теофилом Вандермондом, который явно отметил важность топологических особенностей при обсуждении свойств узлов, связанных с геометрией положения. Математические исследования узлов начались в 19-м веке с Карла Фридриха Гаусса , который определил связывающий Интеграл ( серебро 2006 ). В 1860-х годах теория лорда Кельвина о том, что атомы являются узлами в эфире, привела к Питеру Гатри Тейтусоздание первых таблиц узлов для полной классификации. В 1885 году Тейт опубликовал таблицу узлов, насчитывающую до десяти пересечений, и то, что стало известно как "гипотезы Тайта". Эта запись мотивировала ранних теоретиков узла, но теория узла в конечном счете стала частью появляющегося предмета топологии .
Эти топологи в начале 20— го века—Макс Ден , Я. W. Александр и другие-изучали узлы с точки зрения группы узлов и инвариантов из теории гомологии , таких как многочлен Александра . Это было бы основным подходом к теории узлов до тех пор, пока ряд прорывов не трансформировал предмет.
В конце 1970-х Уильям Терстон ввел гиперболическую геометрию в исследование узлов с теоремой гиперболизации . Было показано, что многие узлы являются гиперболическими узлами, что позволяет использовать геометрию для определения новых мощных инвариантов узлов . Открытие многочлена Джонса Воаном Джонсом в 1984 году ( Соссинский 2002, с. 71-89) и последующие вклады Эдварда Виттена, Максима Концевича и других, выявили глубокие связи между теорией узлов и математическими методами в статистической механике и квантовой теории поля. С тех пор было изобретено множество инвариантов узлов, использующих сложные инструменты, такие как квантовые группы и гомологии Флоера .
В последние несколько десятилетий 20-го века ученые заинтересовались изучением физических узлов, чтобы понять явления завязывания узлов в ДНК и других полимерах. Теория узлов может использоваться, чтобы определить, является ли молекула хиральной (имеет "handedness") или нет ( Simon 1986 ). Путать, строки с обоими концами зафиксированными в месте, эффектно были использованы в изучать действие topoisomerase на дна (Flapan 2000 ). Теория узлов может иметь решающее значение в построении квантовых компьютеров с помощью модели топологических квантовых вычислений ( Collins 2006 ).
Эквивалентность узла[править]


Узел создается, начиная с одномерного отрезка линии, обертывая его вокруг себя произвольно, а затем сплавляя его два свободных конца вместе, чтобы сформировать замкнутую петлю ( Adams 2004 ) ( Sossinsky 2002 ). Просто мы можем сказать, что узел K Тысяча- это "простая замкнутая кривая" или "(замкнутая) Жордановая кривая" (см. кривая), то есть "почти" инъективная и непрерывная функция K : [ 0 , 1 ] → R 3 , с единственной "неинъективностью" K ( 0 ) = K ( 1 ) K (0)=K (1). Топологи полагают, что узлы и другие запутывания, такие как связи и косы, эквивалентны, если узел может быть выдвинут гладко, не пересекая себя, чтобы совпасть с другим узлом.
Идея эквивалентности узлов состоит в том, чтобы дать точное определение того, когда два узла следует считать одинаковыми, даже если они расположены совершенно по-разному в пространстве. Формальное математическое определение состоит в том, что два узла K 1 , K 2 , K_{2}}эквивалентны, если существует гомеоморфизм h : R 3 → R 3 {}с сохранением ориентации h ( K 1 ) = K 2 )=K_{2}} )=K_{2}}.
Другой способ определить эквивалентность узлов состоит в том, что два узла эквивалентны, когда существует непрерывное семейство гомеоморфизмов {h T : R 3 → r 3 Для 0 ≤ T ≤ 1} пространства на себя, так что последний из них несет первый узел на второй узел. (Более формально: два узла к1 и к2 являются эквивалентными , если существует непрерывное отображение Н: Р3× [0,1] → Р3 , такие, что а) для каждого Т ∈ [0,1] отображение принимая х ∈ р3 К Н(Х,Т) ∈ Р3 - это гомеоморфизма от Р3 на себя; б) ч(Х, 0) = х для всех Х ∈ р3; и C) ч.(К1,1) = к2. Такая функция H известна как окружающая изотопия .)
Эти два понятия эквивалентности узла соглашаются точно о том, какие узлы эквивалентны: два узла, которые эквивалентны под сохраняющим ориентацию определением гомеоморфизма, также эквивалентны под окружающим определением изотопии, потому что любые сохраняющие ориентацию гомеоморфизмы R 3 сама по себе является заключительной стадией окружающей изотопии, начинающейся с идентичности. И наоборот, два узла, эквивалентные по определению окружающей изотопии, также эквивалентны по определению гомеоморфизма сохранения ориентации, потому что T=1 (заключительная) стадия окружающей изотопии должна быть гомеоморфизмом сохранения ориентации, несущим один узел к другому.
Основная проблема теории узлов, проблема распознавания, заключается в определении эквивалентности двух узлов. Алгоритмы существуют, чтобы решить эту проблему с первым данным Вольфгангом Хакеном в конце 1960-х (Hass 1998 ). Тем не менее, эти алгоритмы могут быть чрезвычайно трудоемкими, и основной проблемой в теории является понимание того, насколько эта проблема действительно сложна ( Hass 1998 ). Особый интерес представляет особый случай распознавания неизвестного, называемый проблемой неизвестности ( Hoste 2005 ).
Диаграммы узлов[править]
Полезным способом визуализации и управления узлами является проецирование узла на плоскость—подумайте о узле, отбрасывающем тень на стену. Небольшое изменение в направлении проекции гарантирует, что она взаимно однозначна , за исключением двойных точек, называемых перекрестками, где "тень" узла пересекает себя один раз поперечно ( Rolfsen 1976 ). На каждом пересечении, чтобы быть в состоянии воссоздать оригинальный узел, сверх-прядь должна быть отличена от под-пряди. Это часто делается путем создания разрыва в пряди, идущей внизу. Полученная диаграмма представляет собой плоскую погруженную кривую с дополнительными данными о том, какая прядь закончилась и которая находится под каждым пересечением. (Эти диаграммы называются диаграммами узлов, когда они представляют узел, и диаграммами связей, когда они представляют связь .) Аналогично, узловатые поверхности в 4-пространстве могут быть связаны с погруженными поверхностями в 3-пространстве .
Уменьшенная диаграмма-это узловая диаграмма, в которой нет приводимых пересечений (также нугаторных или съемных пересечений) или в которой все приводимые пересечения были удалены.(Weisstein, ReducedKnotDiagram) (Weisstein, ReducibleCrossing)
Reidemeister перемещается[править]
Главная статья: движение Reidemeister
В 1927, работая с этой диаграммной формой узлов, J. W. Александр и Гарланд Бэйрд Бриггс, и независимо Курт Рейдемейстер , продемонстрировали, что две диаграммы узлов, принадлежащие тому же самому узлу, могут быть связаны последовательностью трех видов движений на диаграмме, показанной ниже. Эти операции, теперь называемые рейдемейстер движется, являются:
- Скрутите и раскрутите в любом направлении.
- Переместите одну прядь полностью на другую.
- Переместите прядь полностью над или под пересечением.
Reidemeister движется
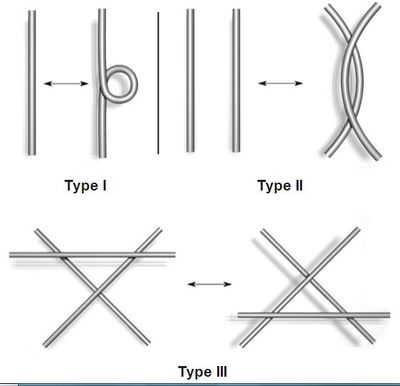
Доказательство того, что диаграммы эквивалентных узлов связаны рейдемейстеровскими движениями, основывается на анализе того, что происходит под плоской проекцией движения, приводящего один узел к другому. Движение может быть устроено так, что почти все время проекция будет диаграммой узлов, за исключением конечного числа раз, когда происходит "событие" или "катастрофа", например, когда более двух нитей пересекаются в точке или несколько нитей становятся касательными в точке. Тщательный осмотр покажет, что сложные события могут быть устранены, оставив только самые простые события: (1) "излом", образующий или выпрямляемый; (2) две нити, становящиеся касательными в точке и проходящие через; и (3) три нити, пересекающиеся в точке. Это как раз шаги Рейдемайстера ( Sossinsky 2002 , ch. 3) (Lickorish 1997 , ch. 1). Инварианты узла Главная статья: инвариант узла
Инвариант узла-это" количество", одинаковое для эквивалентных узлов ( Adams 2004 ) ( Lickorish 1997 ) ( Rolfsen 1976 ). Например, если инвариант вычисляется из Узловой диаграммы, он должен давать одинаковое значение для двух узловых диаграмм, представляющих эквивалентные узлы. Инвариант может принимать одинаковое значение на двух разных узлах, поэтому сам по себе он может быть неспособен различать все узлы. Элементарным инвариантом является трехцветность .
"Классические" инварианты узла включают группу узлов , которая является фундаментальной группой дополнения узла , и многочлен Александра, который может быть вычислен из инварианта Александра, модуля, построенного из бесконечного циклического покрытия дополнения узла ( Lickorish 1997 )( Rolfsen 1976 ). В конце 20-го века были обнаружены инварианты, такие как "квантовые" узловые полиномы, инварианты Васильева и гиперболические инварианты. Эти вышеупомянутые инварианты являются лишь верхушкой айсберга современной теории узлов.
Многочлены узла[править]
Главная статья: многочлен узла
Многочлен узла-инвариант узла, который является многочленом . Известные примеры включают многочлены Джонса и Александра . Вариант многочлена Александера, многочлен Александера-Конвея, является многочленом в переменной z с целыми коэффициентами (Lickorish 1997 ).
Многочлен Александера-Конвея фактически определяется в терминах связей, которые состоят из одного или нескольких узлов, запутанных друг с другом. Понятия, объясненные выше для узлов, например диаграммы и движения Reidemeister, также держатся для связей.
Рассмотрим ориентированную диаграмму связи, т. е. такую, в которой каждый компонент связи имеет предпочтительное направление, обозначенное стрелкой. Для данного пересечения диаграммы позвольте L + , L − , L 0 ,L_{-},L_{0}} L_ {+}, L_ { - }, L_{0}быть ориентированными диаграммами связи, являющимися результатом изменения диаграммы, как показано на рисунке:
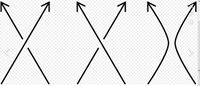
Исходная диаграмма может быть либо L + Л+_или L − Л_-, в зависимости от конфигурации выбранного пересечения. Тогда многочлен Александера-Конвея C ( z ) C (z)рекурсивно определяется в соответствии с правилами:
- C ( O ) = 1 C (O) = 1 (где O Oлюбая диаграмма неизвестного)
- C ( L + ) = C ( L − ) + z C ( L 0 ) .
Второе правило-это то, что часто называют отношением мотка . Чтобы проверить, что эти правила дают инвариант ориентированной связи, следует определить, что полином не изменяется при трех движениях Рейдемейстера. Таким образом, можно определить многие важные многочлены узлов.
Ниже приведен пример типичного вычисления с использованием отношения мотков. Он вычисляет многочлен Александера-Конвея узла трилистника . Желтые пятна указывают, где применяется отношение.

это означает, что C (unlink of two components) = 0, так как первые два многочлена имеют неизвестное и, следовательно, равны.
Сложив все это воедино покажет:
- C (трилистник) = 1 + z (0 + z) = 1 + z 2 .
Поскольку многочлен Александера–Конвея является инвариантом узла, это показывает, что трилистник не эквивалентен неизвестному. Таким образом, трилистник действительно "завязан".

Фактически, есть два узла трилистника, названные правыми и левыми трилистниками, которые являются зеркальными отображениями друг друга (возьмите диаграмму трилистника, данного выше, и измените каждое пересечение на другой способ получить зеркальное изображение). Они не эквивалентны друг другу, что означает, что они не являются амфихейными. Это было показано Максом Деном, до изобретения узловых многочленов, с использованием групповых теоретических методов (Dehn 1914 ). Но многочлен Александера-Конвея каждого вида трилистника будет таким же, как видно из приведенного выше вычисления с зеркальным отображением. Джонс многочлен может фактически различать левые и правые узлы трилистника (Lickorish 1997 ).
Гиперболические инварианты[править]
Уильям Терстон доказал, что многие узлы являются гиперболическими узлами, что означает, что дополнение узла (т. е. множество точек 3-пространства не на узле) допускает геометрическую структуру, в частности гиперболическую геометрию . Гиперболическая структура зависит только от узла, поэтому любая величина, вычисленная из гиперболической структуры, является инвариантом узла ( Adams 2004 ).

Геометрия позволяет нам визуализировать, как выглядит внутренняя часть узла или дополнения связи, представляя световые лучи как движущиеся вдоль геодезических геометрии. Пример представлен изображением дополнения борромовых колец . Обитатель этого дополнения связи просматривает пространство вблизи Красного компонента. Шары на картинке-виды horoball окрестности ссылки. Путем сгущения связи стандартным способом получены окрестности horoball компонентов связи. Несмотря на то, что граница окрестности является Тором, если смотреть изнутри дополнения ссылки, она выглядит как сфера. Каждый компонент связи показывает как бесконечно много сфер (одного цвета), так и бесконечно много световых лучей от наблюдателя к компоненту связи. Фундаментальный параллелограмм (который обозначен на рисунке), выложен как вертикально, так и горизонтально и показывает, как бесконечно расширять узор сфер.
Этот шаблон, шаблон horoball, сам по себе является полезным инвариантом. Другие гиперболические инварианты включают форму фундаментального параллелограмма,длину кратчайшей геодезической и объем. Современные усилия по табуляции узлов и связей эффективно использовали эти инварианты. Быстрые компьютеры и умные методы получения этих инвариантов делают вычисление этих инвариантов на практике простой задачей ( Adams, Hildebrand & Weeks 1991 ). Более высокие размеры
Узел в трех измерениях может быть развязан при размещении в четырехмерном пространстве. Это делается путем смены переходов. Предположим, что одна нить находится за другой, если смотреть из выбранной точки. Поднимите его в четвертое измерение, чтобы не было никаких препятствий (передняя прядь не имеет компонента); затем сдвиньте ее вперед и отбросьте назад, теперь спереди. Аналогии для самолета будут поднимать строку с поверхности или удалять точку из круга.
Фактически, в четырех измерениях любой непересекающийся замкнутый контур одномерной струны эквивалентен неизвестному. Сначала "протолкните" петлю в трехмерное подпространство, которое всегда можно, хоть и технически объяснить. Завязывание сфер более высокого размера
Поскольку узел можно рассматривать топологически как 1-мерную сферу, следующим обобщением является рассмотрение двумерной сферы ( S2), вложенной в 4-мерное Евклидово пространство ( R4 ). Такое вложение завязывается, если нет гомеоморфизма R 4 на себя, принимая вложенную 2-сферу к стандартному "круглому" вложению 2-сферы. Суспендировать узлы и закрученные узлы 2 типичных семейства таких узлов 2 сфер.
Математическая техника, называемая "общим положением", подразумевает, что для данной n-сферы в m-мерном Евклидовом пространстве, если m достаточно велико (в зависимости от n), сфера должна быть развязана. В общем случае кусочно-линейные n-сферы образуют узлы только в ( n + 2)-мерном пространстве (Zeeman 1963 ), хотя это больше не является требованием для гладко завязанных сфер. Фактически, в 6K − мерном пространстве есть гладко завязанные (4 K-1)- сферы, например, в R 6 есть гладко завязанная 3-сфера (Haefliger 1962 )( Levine 1965). Таким образом, коразмерность гладкого узла может быть сколь угодно большой, если не фиксировать размерность узловатой сферы; однако любая гладкая K-сфера, вложенная в R n с 2 n − 3 k − 3 > 0, не связана. Понятие узла имеет дальнейшие обобщения в математике, см.: узел (математика) , изотопическая классификация вложений .
Каждый узел в S n является связью вещественно-алгебраического множества с изолированной особенностью в R n +1 (Akbulut & King 1981 ).
N-узел-это один s n, встроенный в R m . N-ссылка - K-копии s n, вложенные в R m, где k-натуральное число. Оба случая m = n + 2 и m > > n + 2 хорошо изучены. Случай N > 1 имеет разные фьючерсы от случая > n = 1 и является захватывающим полем.
Добавление узлов[править]
Главная статья: сумма узла
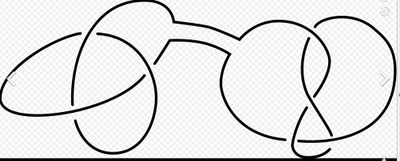
2 узла могут быть добавлены путем резать оба узла и соединять пары концов. Операция называется суммой узлов, или иногда связанной суммой или составом двух узлов. Это может быть формально определено следующим образом ( Адамс 2004): рассмотрим плоскую проекцию каждого узла и предположим, что эти проекции непересекаются. Найдите прямоугольник в плоскости, где одна пара противоположных сторон является дугами вдоль каждого узла, в то время как остальная часть прямоугольника отделена от узлов. Сформируйте новый узел, удалив первую пару противоположных сторон и примыкая к другой паре противоположных сторон. Полученный узел представляет собой сумму исходных узлов. В зависимости от того, как это делается, могут возникнуть два разных узла (но не более). Эта двусмысленность в сумме может быть устранена относительно узлов как ориентированных, т. е. имеющие предпочтительное направление перемещения вдоль узла, и требующие дуги узлов в сумме ориентируются последовательно с ориентированной границей прямоугольника.
Сумма узлов ориентированных узлов коммутативна и ассоциативна . Узел является простым, если он нетривиален и не может быть записан как сумма узлов двух нетривиальных узлов. Узел, который может быть записан как такая сумма, является составным . Существует простое разложение для узлов, аналогичное простым и составным числам (Schubert 1949 ). Для ориентированных узлов это разложение также уникально. Узлы более высокого размера также могут быть добавлены, но есть некоторые различия. Хотя вы не можете сформировать unknot в трех измерениях, добавив два нетривиальных узла, вы можете в более высоких измерениях, по крайней мере, когда один считает гладким узлов в коразмерности не менее 3.
Табулирование узлов[править]
См. также: список основных узлов и таблица узлов
Традиционно узлы каталогизированы по количеству пересечений. Таблицы узлов обычно включают только основные узлы и только одну запись для узла и его зеркального отображения (даже если они отличаются) ( Hoste, Thistlethwaite & Weeks 1998 ). Число нетривиальных узлов данного числа пересечений быстро увеличивается, что затрудняет вычисление таблиц ( Hoste 2005, p. 20). Усилия по составлению таблиц увенчались успехом в перечислении более 6 миллиардов узлов и звеньев ( Hoste 2005 p. 28). Последовательность числа простых узлов данного числа пересечений, вплоть до числа пересечений 16, равна 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46 972 , 253 293 , 1 388 705 ... (последовательность A002863 в OEIS). Хотя экспоненциальные верхняя и нижняя границы для этой последовательности известны, не было доказано, что эта последовательность строго увеличивается ( Adams 2004 ).
Первые таблицы узлов Tait, Little и Kirkman использовали диаграммы узлов, хотя Tait также использовал предшественник нотации Dowker . Различные обозначения были изобретены для узлов, которые позволяют более эффективное табулирование (Hoste 2005 ).
Ранние таблицы попытались перечислить все узлы максимум 10 пересечений и все чередующиеся узлы 11 пересечений ( Hoste, Thistlethwaite & Weeks 1998 ). Развитие теории узлов благодаря Александру, Рейдемайстеру, Зайферту и другим облегчило задачу верификации, а таблицы узлов вплоть до 9 пересечений были опубликованы Александром–Бриггсом и Рейдемайстером в конце 1920-х годов.
Первая крупная проверка этой работы была сделана в 1960–х годах Джоном Хортоном Конвеем , который не только разработал новую нотацию, но и многочлен Александера-Конвея ( Conway 1970 ) ( Doll & Hoste 1991 ). Это проверило список узлов максимум 11 пересечений и новый список связей до 10 пересечений. Конвей нашел много упущений, но только одно дублирование в Tait–маленьких таблицах; однако он пропустил дубликаты, названные парой Perko , которая будет только замечена в 1974 Кеннетом Перко ( Perko 1974). Эта знаменитая ошибка распространилась бы, когда Дейл Рольфсен добавил таблицу узлов в свой влиятельный текст, основанный на работе Конвея. Статья Конвея 1970 года по теории узлов также содержит типографское дублирование на его неперемежающейся странице с 11 пересекающимися узлами и опускает 4 примера-2, ранее перечисленные в Принстонской старшей диссертации Д. Ломбардеро 1968 года и еще 2, впоследствии обнаруженных Аленом Кодроном. [см.Perko (1982), Primality of sertain knots, Topology Proceedings] менее известен дубликат в его таблице 10 crossing link: 2.-2.-20.20-зеркало 8*-20: -20. [См. Perko (2016), исторические моменты нециклической теории узлов, J. разветвления теории узлов].
В конце 1990-х Hoste, Thistlethwaite и Weeks составили таблицу всех узлов через 16 пересечений ( Hoste, Thistlethwaite & Weeks 1998 ). В 2003 Рэнкин, Флинт и Шерманн, составили таблицу переменных узлов через 22 пересечения ( Hoste 2005 ). Нотация Александра-Бриггса
Это-самая традиционная нотация, из-за бумаги 1927 года Джеймса В. Александра и Гарланда Б. Бриггса и позже расширенного Дейлом Рольфсеном в его таблице узла (см. изображение выше и список главных узлов ). Обозначение просто организует узлы по их числу пересечения. Один пишет номер пересечения с индексом, чтобы обозначить его порядок среди всех узлов с этим номером пересечения. Этот порядок произволен и поэтому не имеет особого значения (хотя в каждом числе пересечений узел скручивания приходит после узла Тора). Ссылки записываются номером пересечения с надстрочным индексом для обозначения количества компонентов и индексом для обозначения его порядка в ссылках с таким же количеством компонентов и пересечений. Таким образом, узел трилистника обозначен 3 1, а звено Хопфа-2 2 1 .
Нотация даукера[править]
Главная статья: нотация Даукера

Обозначение Даукера, также называемое обозначением Даукера-Тислтуэйта или кодом, для узла является конечной последовательностью четных целых чисел. Числа генерируются путем следования за узлом и маркировки пересечений последовательными целыми числами. Так как каждое пересечение посещается дважды, это создает спаривание четных чисел с нечетными. Соответствующий знак дан, чтобы указать на чрезмерное и недостаточное пересечение. Например, на этом рисунке диаграмма узлов имеет пересечения, помеченные парами (1,6) (3,-12) (5,2) (7,8) (9,-4) и (11,-10). Обозначение Dowker для этой маркировки-это последовательность: 6, -12, 2, 8, -4, -10. Диаграмма узлов имеет более одной возможной нотации Даукера, и существует хорошо понятная двусмысленность при восстановлении узла из нотации Даукера.
Нотация Конвея[править]
Основная статья: нотация Конвея (теория узлов)
Нотация Конвея для узлов и связей, названная в честь Джона Хортона Конвея , основана на теории путаницы ( Conway 1970 ). Преимущество этой нотации заключается в том, что она отражает некоторые свойства узла или связи.
Нотация описывает, как построить определенную диаграмму связи связи. Начните с основного многогранника, 4-валентного Связного плоского графа без областей дигона. Такой многогранник обозначается сначала числом вершин, затем числом звездочек, определяющих положение многогранника в списке основных многогранников. Например, 10 * * обозначает второй 10-вершинный многогранник в списке Конвея.
Каждая вершина тогда имеет алгебраический клубок, замененный в нее (каждая вершина ориентирована так, что нет произвольного выбора в замене). Каждый такой клубок имеет обозначение, состоящее из цифр и знаков + или -.
Примером является 1*2 -3 2... 1 * обозначает единственный 1-вершинный основной многогранник. 2 -3 2-Последовательность, описывающая непрерывную часть, связанную с рациональным клубком . Один вставляет этот клубок в вершину основного многогранника 1*.
Более сложный пример 8*3.1.2 0.1.1.1.1.1.1.1 здесь снова 8 * относится к основному многограннику с 8 вершинами. Периоды разделяют обозначения для каждого клубка.
Любая ссылка допускает такое описание, и понятно, что это очень компактное обозначение даже для очень большого числа пересечений. Есть еще несколько сокращений, которые обычно используются. Последний пример обычно пишется 8*3: 2 0, где те опущены и сохранены число точек за исключением точек в конце. Для алгебраического узла, такого как в первом примере, 1* часто опускается.
Новаторская статья Конвея по этому вопросу перечисляет до 10-вершинных базовых многогранников, из которых он использует для табуляции ссылок, которые стали стандартными для этих ссылок. Для дальнейшего перечисления более высоких вершинных многогранников доступны нестандартные варианты.
Код Гаусса[править]
Код Гаусса, подобный нотации Даукера, представляет собой узел с последовательностью целых чисел. Однако вместо того, чтобы каждое пересечение было представлено двумя разными номерами, пересечение помечается только одним номером. Когда пересечение является пересечением, указывается положительное число. При перекрещивании отрицательное число.
Например, узел трилистника в коде Гаусса может быть задан как: 1, -2,3, -1,2, -3
Код Гаусса ограничен в своей способности идентифицировать узлы несколькими проблемами. Начальная точка на узле, с которой начинается трассировка пересечений, произвольна, и нет способа определить, в каком направлении отслеживать. Кроме того, код Гаусса не может указывать на управляемость каждого пересечения, что необходимо для идентификации узла по сравнению с его зеркалом. Например, код Гаусса для узла трилистника не указывает, является ли он правым или левым трилистником.
Эта последняя проблема часто решается с помощью расширенного кода Гаусса. В этом изменении положительный / отрицательный знак на втором экземпляре каждого числа выбран, чтобы представлять управляемость того пересечения, а не по/Под знаком пересечения, которое ясно в первом экземпляре числа. Правому перекрестку присваивается положительное число, а левому перекрестку-отрицательное.
См. также[править]
- Контактная геометрия#Legendrian подмногообразия и узлы
- Узлы и графики
- Список тем теории узлов
- Молекулярный узел
- Квантовые узлы
- Квантовая топология
- Теория ленты
- Галстук § виды узлов
Дальнейшее чтение[править]
Вводные учебники
Существует ряд введений в теорию узлов. Классическое введение для аспирантов или продвинутых магистрантов ( Rolfsen 1976 ). Другие хорошие тексты из ссылок ( Adams 2001 ) и ( Lickorish 1997 ). Адамс неформален и доступен по большей части старшеклассникам. Lickorish-строгое введение для аспирантов, охватывающее приятное сочетание классических и современных тем.
- Burde, Gerhard ; Zieschang, Heiner (1985), узлы, исследования де Грюйтера в математике, 5, Вальтер де Грюйтер,
- Кроуэлл, Ричард Х.; Фокс, Ральф (1977). Введение в теорию узлов . .
- Kauffman, Louis H. (1987), на узлах,
- Kauffman, Louis H. (2013), узлы и физика (4-е изд.), World Scientific,
Опросы
- Менаско, Уильям У.; Thistlethwaite, Morwen, eds. (2005), справочник теории узлов, Elsevier,
- Руководство Menasco и Thistlethwaite рассматривает смесь тем, имеющих отношение к текущим тенденциям исследования способом, доступным для продвинутых студентов, но представляющих интерес для профессиональных исследователей.
- Livio, Mario (2009), "Ch. 8: Необоснованная Эффективность?- Бог-математик?, Simon & Schuster, PP. 203-218,