Чудовищный самогон

В математикечудовищный самогон, или теория самогона, - это неожиданная связь между группой монстров M и модулярными функциями, в частности, функцией j. Этот термин был введен Джоном Конвеем и Саймоном Нортоном в 1979 году.

Теперь известно , что за чудовищным лунным светом лежит вершинная операторная алгебра , называемая модулем лунного света (или вершинной алгеброй монстра), построенная Игорем Френкелем, Джеймсом Леповскими Арне Мерманом в 1988 году, имеющая группу монстров в качестве симметрий. Эта вершинная операторная алгебра обычно интерпретируется как структура , лежащая в основе двумерной конформной теории поля, позволяющая физике образовать мост между двумя математическими областями. Гипотезы, сделанные Конвеем и Нортоном, были доказаны Ричардом Борчердсом для модуля moonshine в 1992 году с использованием теоремы об отсутствии призраков из теории струн а также теория вершинных операторных алгебр и обобщенных алгебр Каца–Муди.

История

В 1978 году Джон Маккей обнаружил, что первые несколько членов в разложении Фурье нормализованного J-инварианта (последовательность A014708 в OEIS),

   J ( τ ) = 1 q + 196884 q + 21493760 q 2 + 864299970 q 3 + 20245856256 q 4 + ⋯ 

С q = e 2 π i τ }и τ в качестве полупериодического отношения можно было бы выразить в терминах линейных комбинаций размерностей неприводимых представлений r n группы монстров M (последовательность A001379 в OEIS) с малыми неотрицательными коэффициентами. Пусть r n r_{n}= 1, 196883, 21296876, 842609326, 18538750076, 19360062527, 293553734298, ... затем,

оп

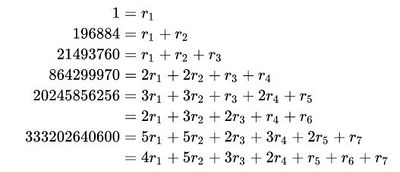
   1 = r 1 
196884 = r 1 + r 2 
21493760 = r 1 + r 2 + r 3 
864299970 = 2 r 1 + 2 r 2 + r 3 + r 4 
20245856256 = 3 r 1 + 3 r 2 + r 3 + 2 r 4 + r 5 
= 2 r 1 + 3 r 2 + 2 r 3 + r 4 + r 6 
333202640600 = 5 r 1 + 5 r 2 + 2 r 3 + 3 r 4 + 2 r 5 + r 7 
= 4 r 1 + 5 r 2 + 3 r 3 + 2 r 4 + r 5 + r 6 + r 7 

(Поскольку между такими как может быть несколько линейных отношений r n r_{n} r 1 − r 3 + r 4 + r 5 − r 6 = 0 , представление может быть более чем одним способом.) Маккей рассматривал это как доказательство того , что существует естественно возникающее бесконечномерное градуированное представление M, градуированная размерность которого задается коэффициентами Jи части которого с меньшим весом разлагаются на неприводимые представления, как указано выше. После того, как он сообщил Джону г. Томпсону об этом наблюдении, Томпсон предположил, что поскольку градуированное измерение - это просто градуированный след элемента тождества, градуированные следы нетривиальных элементов g из M о таком представлении тоже может быть интересно.

Конвей и Нортон вычислили члены более низкого порядка таких градуированных следов, теперь известных как серия Маккея-Томпсона Tg, и обнаружили, что все они, по-видимому, являются разложениями Гауптмодульна. Другими словами, если Gg является подгруппой SL2(R), которая фиксирует Tg, то частное верхней половины комплексной плоскости Gg является сферой с конечным числом удаленных точек, и, кроме того, TG порождает поле мероморфных функций на этой сфере.

Основываясь на своих вычислениях, Конвей и Нортон составили список Гауптмодульнов и предположили существование бесконечномерного градуированного представления M, градуированные следы которого TG являются разложениями именно функций из их списка.

В 1980 году А. Оливер л. Аткин, пол Фонг и Стивен Д. Смит представили убедительные вычислительные доказательства того, что такое градуированное представление существует, разложив большое число коэффициентов J на представления M. Градуированное представление, градуированная размерность которого равна J, называемое модулем лунного света, было явно построено Игорем Френкелем, Джеймсом Леповскими Арне Мерманом, дающим эффективное решение гипотезы Маккея-Томпсона, а также они определили градуированные следы для всех элементов централизатора инволюции M, частично разрешив гипотезу Конвея-Нортона. Кроме того, они показали , что построенное ими векторное пространство , называемое модулем лунного V ♮ V^\натуральныйсвета, имеет дополнительную структуру вершинной операторной алгебры, группа автоморфизмов которой точно равна M.

Борчердс доказал гипотезу Конвея-Нортона для модуля самогона в 1992 году. Он получил медаль Филдса в 1998 году отчасти за свое решение этой гипотезы.

Модуль монстра

Конструкция Френкеля-Леповского-Мермана начинается с двух основных инструментов:

• Построение вершинной операторной алгебры решетки VL для четной решетки L ранга n. В физических терминах это хиральная алгебра для бозонной струны , компактифицированной на Торе Rn/L. Его можно приблизительно описать как тензорное произведение группового кольца L с представлением осциллятора в n измерениях (которое само по себе изоморфно полиномиальному кольцу в счетно бесконечном числе генераторов). Для рассматриваемого случая задается L-решетка пиявки, имеющая ранг 24.
• Конструкция орбифолда. В физических терминах это описывает бозонную струну, распространяющуюся по частному орбифолду. Построение Френкеля–Леповского-Мермана было первым случаем появления орбифолдов в конформной теории поля. Прикрепленный к -1 инволюции решетки пиявки, существует инволюция h VLи неприводимый H-скрученный модуль V L, который наследует инволюцию подъема h. Чтобы получить модуль самогона, нужно взять подпространство неподвижной точки h в прямой сумме VL и его скрученного модуля.

Затем Френкель, Леповский и Мерман показали, что группа автоморфизмов модуля самогона, как вершинная операторная алгебра, равна M. Кроме того, они определили, что градуированные следы элементов в подгруппе 21+24.Co1 соответствует функциям, предсказанным Конвеем и Нортоном (Frenkel, Lepowsky & Meurman (1988)).

Доказательство борхердса

Доказательство Ричарда Борчердса гипотезы Конвея и Нортона можно разбить на следующие основные этапы:

• Начинается с вершинной операторной алгебры V с инвариантной билинейной формой, действием M автоморфизмов и известным разложением однородных пространств семи низших степеней на неприводимые M-представления. Это было обеспечено конструкцией и анализом модуля самогона Френкеля–Леповского–Мермана.
• Алгебра m }ли, называемая чудовищной алгебройли, строится из V с использованием функтора квантования. Это обобщенная алгебра ли Каца-Муди с чудовищным действием автоморфизмов. Используя теорему Годдарда-Торна "без призрака" из теории струн, корневые кратности оказываются коэффициентами J.
• Для построения обобщенной алгебры ли Каца–Муди с помощью генераторов и соотношений используется тождество бесконечного произведения койке–Нортона–Загье. Тождество доказывается с помощью того факта, что операторы Гекке, примененные к J, дают многочлены в J.
• Сравнивая кратности корней, можно обнаружить, что две алгебры ли изоморфны, и в частности, формула знаменателя Вейля Для m }является именно тождеством койке–Нортона–Загье.
• Используя гомологию алгебры Ли и операции Адамса, для каждого элемента задается скрученное тождество знаменателя. Эти тождества связаны с серией Маккея-Томпсона Tg во многом так же, как тождество койке–Нортона–Загье связано с J.
• Скрученные тождества знаменателя подразумевают рекурсивные отношения на коэффициентах Tg, и неопубликованная работа койке показала, что кандидатные функции Конвея и Нортона удовлетворяют этим рекурсивным отношениям. Эти отношения достаточно сильны, чтобы проверить, согласуются ли первые семь членов с функциями, заданными Конвеем и Нортоном. Наименьшие члены задаются разложением семи однородных пространств наименьшей степени, заданных на первом шаге.

Таким образом, доказательство завершено (Borcherds (1992)). Позже борчердс цитировал: "я был на седьмом небе, когда доказал гипотезу о самогоне", и "иногда я задаюсь вопросом, не такое ли это чувство возникает, когда вы принимаете определенные наркотики. На самом деле я не знаю, так как не проверял эту свою теорию."(Roberts 2009, p. 361)

Более поздняя работа упростила и прояснила последние шаги доказательства. Юрисич (Jurisich (1998), Jurisich, Lepowsky & Wilson (1995)) обнаружил, что вычисление гомологии можно существенно сократить, заменив обычное треугольное разложение чудовищной алгебры ли разложением на сумму gl2 и двух свободных алгебр Ли. Камминс и Гэннон показали, что рекурсивные соотношения автоматически подразумевают, что ряды Маккея Томпсона либо Гауптмодульны, либо заканчиваются не более чем через 3 члена, что устраняет необходимость в вычислениях на последнем шаге.

Обобщенный самогон

Конвей и Нортон предположили в своей работе 1979 года, что, возможно, лунный свет не ограничивается монстром, но что подобные явления могут быть обнаружены для других групп.хотя утверждения Конвея и Нортона не были очень конкретными, вычисления Лариссы Куин в 1980 году убедительно показали, что можно построить разложения многих Гауптмодулей из простых комбинаций размерностей неприводимых представлений спорадических групп. В частности, она разложила коэффициенты ряда Маккея-Томпсона на представления субквотентов монстра в следующих случаях:

• T2B и T4A в представления группы Конвея Co0
• T3B и T6B в представления группы Suzuki 3.2.Сюз
• T3C в представления группы Томпсона Th = F3
• T5A в представления группы Харада-Нортона HN = F5
• T5B и T10D в представления группы Холла-Янко 2.HJ
• T7A в представления удерживаемой группы He = F7
• T7B и T14C в представления 2.А7
• T11A в представления группы Матье 2.М12

Куин обнаружил, что следы неидентичных элементов также дают q-расширения Гауптмодульна, некоторые из которых не были сериями Маккея-Томпсона из монстра. В 1987 году Нортон объединил результаты Queen со своими собственными вычислениями, чтобы сформулировать обобщенную гипотезу самогона. Эта гипотеза утверждает, что существует правило, которое присваивает каждому элементу G монстра градуированное векторное пространство V(g), а каждой коммутирующей паре элементов (g,h) голоморфную функцию f(g,h, τ ) на верхней полуплоскости, такую, что:

• Каждый V(g) является градуированным проективным представлением централизатора g в M.
• Каждый f(g,h, τ) является либо постоянной функцией, либо Гауптмодулем.
• Каждый f(g,h,τ) инвариантен при одновременном сопряжении g и h в M, вплоть до скалярной неоднозначности.
• Для каждого (g,h) существует подъем h к линейному преобразованию на V(g), так что разложение f(g,h, τ) задается градуированным следом.
• Для любого ( a b c d ) ∈ S L 2 ( Z ) )пропорционально f ( g a h c , g b h d , τ ) пропорционально J тогда и только тогда, когда g = h = 1.

Это обобщение гипотезы Конвея-Нортона, поскольку теорема Борхердса касается случая, когда g устанавливается в тождество.

Как и гипотеза Конвея–Нортона, обобщенный самогон также имеет интерпретацию в физике, предложенную Диксоном-Гинспаргом-Харви в 1988 году (Dixon, Ginsparg & Harvey (1989)). Они интерпретировали векторные пространства V(g) как скрученные сектора конформной теории поля с чудовищной симметрией и интерпретировали функции f(g,h, τ) как функции разбиения первого рода, где образуется Тор путем склеивания вдоль скрученных граничных условий. На математическом языке скрученные секторы являются неприводимыми скрученными модулями, а функции разбиения назначаются эллиптическим кривым с главными расслоениями монстров , тип изоморфизма которых описывается монодромией по базису 1-циклов, то есть парой коммутирующих элементов.

Модульный самогон

В начале 1990-х годов теоретик групп А. Я. Е. рыба обнаружил замечательное сходство между частями таблицы символов монстра и персонажами Брауэра некоторых подгрупп. В частности, для элемента g простого порядка p в Монстре многие неприводимые символы элемента порядка kp, k-я степень которого равна g, являются простыми комбинациями символов Брауэра для элемента порядка k в централизаторе g. Это было численное доказательство явления, похожего на чудовищный самогон, но для представлений в положительной характеристике. В частности, рыба предположил в 1994 году, что для каждого простого фактора p в порядке монстра существует градуированная вершинная алгебра над конечным полем Fp с действием централизатора элемента порядка p g, такого что градуированный характер Брауэра любого p-регулярного автоморфизма h равен ряду Маккея-Томпсона для gh (Ryba (1996)).

В 1996 году Борхердс и рыба переосмыслили гипотезу как утверждение о когомологиях Тейта самодвойственной интегральной формы V ♮ {\displaystyle V^{\natural }} V^\натуральный. Эта интегральная форма не была известна, но они построили самодвойственную форму над Z[1/2], что позволило им работать с нечетными простыми числами p. Когомологии Тейта для элемента простого порядка естественно имеют структуру супер вершинной алгебры над Fp, и они разбили проблему на легкий шаг, приравнивающий градуированную супертрассу Брауэра к серии Маккея-Томпсона, и жесткий шаг, показывающий, что когомологии Тейта исчезают в нечетной степени. Они доказали исчезающее утверждение для малых нечетных простых чисел, перенеся исчезающий результат из решетки пиявки (Borcherds & Ryba (1996)). В 1998 году Борчердс показал, что исчезновение имеет место для оставшихся нечетных простых чисел , используя комбинацию теории Ходжа и интегрального уточнения теоремы об отсутствии призраков (Borcherds (1998), Borcherds (1999)).

Случай порядка 2 требует существования формы V ♮ V^\натуральныйнад 2-адическим кольцом, то есть конструкции, которая не делится на 2, и в то время об этом не было известно. Остается много дополнительных вопросов без ответа, таких как то, как гипотеза рыбы должна обобщаться на когомологии Тейта составных элементов порядка, и природа любых связей с обобщенным самогоном и другими явлениями самогона.

Предполагаемая связь с квантовой гравитацией

В 2007 году Э. Виттен предположил, что соответствие AdS/CFT дает двойственность между чистой квантовой гравитацией в (2+1)-мерном анти-Ситтеровском пространстве и экстремальными голоморфными CFTs. Чистая гравитация в измерениях 2+1 не имеет локальных степеней свободы, но когда космологическая постоянная отрицательна, в теории есть нетривиальное содержание, связанное с существованием решений черных дыр БТЗ. Экстремальные Кфт, введенные г. Хеном, отличаются отсутствием первичных полей Вирасоро при низкой энергии, и одним из примеров является модуль moonshine.

Согласно предложению Виттена (Witten, 2007), гравитация в пространстве AdS с максимально отрицательной космологической постоянной двойственна AdS/CFT голоморфному CFT с центральным зарядом c=24, а функция разбиения CFT точно равна j-744, т. е. градуированному характеру модуля moonshine. Предположив гипотезу Френкеля-Леповского-Мермана о том, что модуль moonshine является уникальным голоморфным VOA с центральным зарядом 24 и символом j-744 Виттен пришел к выводу, что чистая Гравитация с максимально отрицательной космологической постоянной двойственна монстру CFT. Часть предложения Виттена состоит в том, что первичные поля Вирасоро двойственны операторам, создающим черные дыры, и в качестве проверки согласованности он обнаружил, что в пределе большой массы Бекенштейн-Хокинг полуклассическая оценка энтропии для данной массы черной дыры согласуется с логарифмом соответствующей первичной кратности Вирасоро в модуле лунного света. В маломассивном режиме существует небольшая квантовая поправка к энтропии, например, первичные поля с наименьшей энергией дают LN (196883) ~ 12.19, в то время как оценка Бекенштейна–Хокинга дает 4π ~ 12.57.

Более поздняя работа уточнила предложение Виттена. Виттен предположил, что экстремальные Кфт с большей космологической постоянной могут иметь чудовищную симметрию, очень похожую на минимальный случай, но это было быстро исключено независимой работой Гайотто и Хена. Работа Виттена и Малоуни (Maloney & Witten, 2007) показала, что чистая квантовая гравитация может не удовлетворять некоторым проверкам согласованности, связанным с ее функцией разбиения, если только некоторые тонкие свойства сложных седел не работают благоприятно. Однако Li-Song-Strominger (Li, Song & Strominger (2008)) предположили, что хиральная квантовая теория гравитации, предложенная Маншотом в 2007 году, может иметь лучшие свойства устойчивости, будучи двойственной к хиральной части монстра CFT, то есть алгебре вершин монстра. Дункан-Френкель (Duncan & Frenkel (2009)) представил дополнительные доказательства этой двойственности, используя суммы Радемахера получить ряд Маккея-Томпсона в виде 2+1 мерных функций гравитационного разбиения регуляризованной суммой по глобальным геометриям Тора-изогении. Кроме того, они предположили существование семейства скрученных киральных теорий гравитации, параметризованных элементами монстра, предполагая связь с обобщенными суммами лунного света и гравитационных инстантонов. В настоящее время все эти идеи все еще довольно спекулятивны, отчасти потому, что трехмерная квантовая гравитация не имеет строгой математической основы.

Матье самогон

В 2010 году Тору Эгути, Хироси Оогури и Юджи Тачикава заметили , что эллиптический род поверхности K3 может быть разложен на символы сверхконформной алгебры N =(4,4), так что кратности массивных состояний кажутся простыми комбинациями неприводимых представлений группы Матье M24. Это говорит о том, что существует Сигма-модель конформной теории поля с мишенью K3, несущей симметрию M24. Однако по классификации Мукаи-Кондо нет верного действия этой группы на любую поверхность K3 симплектическими автоморфизмами, и по работе Габердиеля-Гогенеггера-Вольпато, нет никакого верного действия на любую Сигма-модель K3 конформной теории поля, так что появление действия на лежащем в основе гильбертовом пространстве все еще остается загадкой.

По аналогии с серией Маккея-Томпсона Чэн предположил, что как функции множественности, так и градуированные следы нетривиальных элементов M24 образуют фиктивные модульные формы. В 2012 году Ганнон доказал, что все, кроме первой из кратностей, являются неотрицательными интегральными комбинациями представлений M24, а Габердиэль-Перссон–Ронелленфич–Вольпато вычислил все аналоги обобщенных функций самогона, убедительно предположив, что за самогоном Матье стоит некоторый аналог голоморфной конформной теории поля. Кроме того, в 2012 году Чэн, Дункан и Харви собрали численные доказательства того, что явление умбрального самогона, когда семейства макетных модульных форм, по-видимому, присоединяются к решеткам Нимейера. Частный случай решетки A124 дает самогон Матье, но в целом это явление еще не имеет интерпретации в терминах геометрии.

Происхождение термина

Термин "чудовищная самогон" был придуман Конвей, кто, когда сказал Джон Маккей в конце 1970-х, что коэффициент q {вопрос} (а именно 196884) был точно на единицу больше степени из маленьких верных комплексное представление группы монстра (а именно 196883), ответил, что это был "самогон" (в смысле быть сумасшедшей или глупой идеей).таким образом, этот термин относится не только к группе монстров M; он также относится к воспринимаемому сумасшествию сложной взаимосвязи между M и теорией модулярных функций.

Сопутствующие наблюдения

Группа монстров была исследована в 1970-х годах математиками Жан-Пьером Серром, Эндрю Оггом и Джоном г. Томпсоном; они изучали фактор гиперболической плоскости подгруппами SL2(R), в частности нормализатором Γ0(p)+ подгруппы конгруэнтности Гекке Γ0(p) в SL(2,R). Они обнаружили, что на Римановой поверхности , обусловленное принятием коэффициент гиперболической плоскости при Γ0(П)+ имеет род нуль , если и только если Р является 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59 или 71. Когда позже Огг услышал о группе монстров и заметил, что это были именно главные факторы размера M он опубликовал статью, предлагающую бутылку виски Jack Daniel's любому, кто мог бы объяснить этот факт (Ogg (1974)).

См.также

Пиво

Пруф

web.archive.org/web/20061205032152/http://cicma.mathstat.concordia.ca/faculty/cummins/moonshine.refs.html