Круги Вилларсо


В геометрии круги Вильярсо / V iː lːr ˈ s oʊ / - это пара кругов, полученных путем разрезания Тора наклонно через центр под специальным углом. Учитывая произвольную точку на Торе, через нее можно провести четыре окружности. Один находится в плоскости (содержащей точку), параллельной экваториальной плоскости Тора. Другая перпендикулярна ей. Два других-круги Вильярсо. Они названы в честь французского астронома и математика Ивона Вильярсо (1813–1883). Мангейм (1903) показал, что круги Вилларсо соответствуют всем параллельным круглым поперечным сечениям Тора под одним углом, в результате чего он сказал, что полковник Шельхер представил на конгрессе в 1891 году.
Пример[править]
Например, предположим, что главный радиус Тора равен 5, а малый радиус равен 3. Это означает, что Тор является объединением определенных окружностей радиуса три, центры которых находятся на окружности радиуса пять в плоскости xy. Точки На этом Торе удовлетворяют этому уравнению:
- 0 = ( x 2 + y 2 + z 2 + 16 ) 2 − 100 ( x 2 + y 2 ) .
Нарезка с плоскостью z = 0 дает две концентрические окружности, x 2 + y 2 = 2 2 и x 2 + y 2 = 8 2 . Нарезка с плоскостью x = 0 дает два бок о бок круга, ( y − 5) 2 + z 2 = 3 2 и ( y + 5) 2 + z 2 = 3 2 .
Два примера кругов Вильярсо могут быть получены путем нарезки плоскостью 3 x = 4 z . Один центрирован на (0, +3, 0), а другой на (0, -3, 0); оба имеют радиус пять. Они могут быть записаны в параметрической форме
- ( x , y , z ) = ( 4 cos ϑ , + 3 + 5 sin ϑ , 3 cos ϑ )
и
- ( x , y , z ) = ( 4 cos ϑ , − 3 + 5 sin ϑ , 3 cos ϑ ) .
Плоскость среза выбирается касательной к Тору в двух точках при прохождении через его центр. Это касательная ( 16 ⁄ 5 , 0, 12 ⁄ 5 ) и в ( -16 ⁄ 5 , 0, -12 ⁄ 5 ). Угол среза однозначно определяется размерами выбранного Тора. Вращение любой такой плоскости вокруг оси z дает все круги Вильярсо для этого Тора.
Существование и уравнение[править]
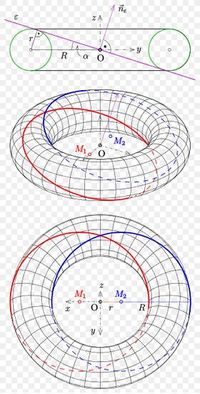
Доказательство существования окружностей можно построить из того, что плоскость среза касательна к Тору в двух точках. Одной из характеристик Тора является то, что он является поверхностью вращения . Без потери общности выберите систему координат так, чтобы ось вращения была осью Z. Начните с окружности радиуса r в плоскости xz, с центром в ( R, 0, 0).
- 0 = ( x − R ) 2 + z 2 − r 2
Подметание заменяет x на (x 2 + y 2 ) 1/2 , а очистка квадратного корня дает уравнение квартики .
- 0 = ( x 2 + y 2 + z 2 + R 2 − r 2 ) 2 − 4 R 2 ( x 2 + y 2 ) .
Поперечное сечение стреловидной поверхности в плоскости xz теперь включает в себя второй круг.
- 0 = ( x + R ) 2 + z 2 − r 2
Эта пара окружностей имеет две общие внутренние касательные линии, с наклоном в начале координат, найденным из прямоугольного треугольника с гипотенузой R и противоположной стороной r (которая имеет прямой угол в точке касания). Таким образом , z / x равен ± r / ( r 2 − r 2 ) 1/2, а выбор знака плюс приводит к уравнению плоскости, битангентной Тору.

- 0 = x r − z R 2 − r 2
По симметрии вращения этой плоскости вокруг оси z дают все битангентные плоскости через центр. (Есть также горизонтальные плоскости, касательные к верхней и нижней части Тора, каждая из которых дает “двойной круг”, но не круги Вильярсо .)
- 0 = x r cos φ + y r sin φ − z R 2 − r 2
Мы можем вычислить пересечение плоскости(плоскостей) с Тором аналитически и, таким образом, показать, что результатом является симметричная пара окружностей, одна из которых является окружностью радиуса R, центрированной в точке
- ( − r sin φ , r cos φ , 0 ) .
Лечение по этим направлениям можно найти в Coxeter (1969).
Более абстрактный и более гибкий подход был описан Hirsch (2002), используя алгебраическую геометрию в проективной настройке. В однородном квартичном уравнении для Тора,
- 0 = ( x 2 + y 2 + z 2 + R 2 w 2 − r 2 w 2 ) 2 − 4 R 2 w 2 ( x 2 + y 2 ) ,
установка w в ноль дает пересечение с "плоскостью на Бесконечности" и уменьшает уравнение до
- 0 = ( x 2 + y 2 + z 2 ) 2 .
Это пересечение-двойная точка, фактически двойная точка, посчитанная дважды. Кроме того, он включен в каждую битангентную плоскость. Две точки касания также являются двойными точками. Таким образом, кривая пересечения, которая, по теории, должна быть квартикой, содержит четыре двойные точки. Но мы также знаем, что квартика с более чем тремя двойными точками должна быть факторной (она не может быть неприводимой), а по симметрии факторами должны быть две конгруэнтные коники . Hirsch распространяет этот аргумент на любой поверхность вращения, порожденная конической, и показывает, что пересечение с битангентной плоскостью должно производить две коники того же типа, что и генератор, когда кривая пересечения реальна. Заполнение пространства
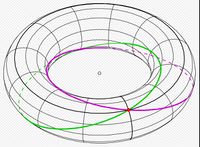
Тор играет центральную роль в расслоении Хопфа 3-сферы, S3, над обычной сферой, S2, которая имеет круги , S1, в качестве волокон. Когда 3-сфера отображается в Евклидово 3-пространство стереографической проекцией, обратное изображение круга широты на S 2 под картой волокон является Тором, а сами волокна являются кругами Вильярсо. Banchoff (1990) исследовал такой Тор с компьютерными графическими изображениями. Один из необычных фактов о кругах заключается в том, что каждый из них связан через все остальные, а не только в своем собственном Торе, но и в коллекции, заполняющей все пространство; Бергер (1987) имеет Обсуждение и рисунок.
См. также[править]
Пруф[править]
.maths-et-physique.net/article-les-cercles-du-tore-38982808.html