Ортогональная проекция

"Ортогональная проекция" перенаправляет сюда. Концепцию технического чертежа смотрите в разделе ортогональная проекция . Конкретное обсуждение ортогональных проекций в конечномерных линейных пространствах см. В разделе Векторная проекция .

В линейной алгебре и функциональном анализе проекция-это линейное преобразование P Пиз векторного пространства в себя такое , что P 2 = P . То есть всякий P Праз, когда он применяется дважды к любому значению, он дает тот же результат, как если бы он был применен один раз ( идемпотент ). Он оставляет свой образ неизменным.[1] хотя это абстрактное определение "проекции" формализует и обобщает идею графической проекции . Можно также рассмотреть влияние проекции на геометрический объект, исследуя влияние проекции на точки в объекте.

Преобразование P является ортогональной проекцией на прямую m .

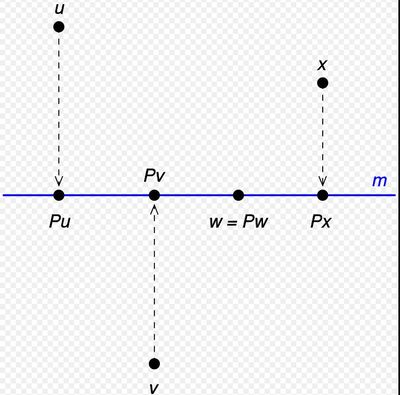
Определения

Проекция на векторное пространство V Вявляется линейным оператором P : V ↦ V , таким что P 2 = P Когда V Вимеет внутреннее произведение и является полным (т. е. Когда V Вявляется гильбертовым пространством), можно использовать понятие ортогональности. Проекция P Пна гильбертово пространство V Вназывается ортогональной проекцией, если она удовлетворяет ⟨ P x , y ⟩ = ⟨ x , P y ⟩ }всем x , y ∈ V x, y\в Vтребованиям . Проекция на гильбертово пространство, которая не является ортогональной, называется косой проекцией .

Проекционная матрица

• В конечномерном случае квадратная матрица P Пназывается проекционной матрицей, если она равна ее квадрату, т. е. если P 2 = P .
• Квадратная матрица P Пназывается ортогональной проекционной матрицей, если P 2 = P = P T для реальной матрицы и соответственно P 2 = P = P H для комплексной матрицы, где P T }обозначает транспозицию P Пи P H обозначает Эрмитову транспозицию P
• Проекционная матрица, которая не является ортогональной проекционной матрицей, называется косой проекционной матрицей .

Собственные значения матрицы проекции должны быть равны 0 или 1.

Примеры

Ортогональная проекция

Например, функция, которая отображает точку ( x , y , z ) )в трехмерном пространстве R 3 }до точки ( x , y , 0 ) , является ортогональной проекцией на плоскость x-Y. Эта функция представлена матрицей

• P = [ 1 0 0 0 1 0 0 0 0 ] . \конец{bmatrix}}.

Действие этой матрицы на произвольный вектор является

• P ( x y z ) = ( x y 0 ) .

Чтобы увидеть, что P Пэто действительно проекция, т. е. P = P 2

• P 2 ( x y z ) = P ( x y 0 ) = ( x y 0 ) = P ( x y z ) .

Наблюдение за этим P T = P показывает, что проекция является ортогональной проекцией.

Косая проекция

Простой пример неортогональной (косой) проекции (для определения см. ниже) является

• P = [ 0 0 α 1 ] .

Через умножение матрицы можно видеть, что

• P 2 = [ 0 0 α 1 ] [ 0 0 α 1 ] = [ 0 0 α 1 ] = P .

доказательство того, что P Пэто действительно проекция.

Проекция P Портогональна тогда и только тогда α = 0 , потому что только тогда P T = P

Свойства и классификация

Идемпотенция

Преобразование T-это проекция вдоль k на m . Диапазон значений T равен m, а нулевое пространство-k .

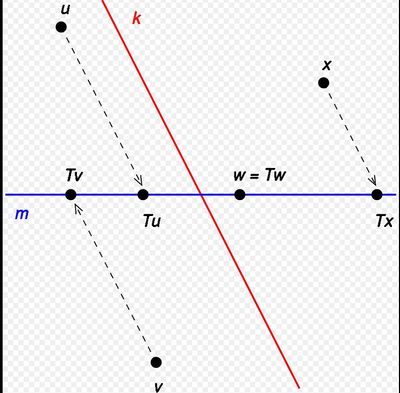
По определению, проекция P Пявляется идемпотентной (т. е. P 2 = P

Комплементарность диапазона и ядра

Пусть W Вэто конечномерное векторное пространство и P Ппроекция на W Внего . Предположим, что подпространства U Uи V Вявляются диапазоном и ядром P Псоответственно. Тогда P Пимеет следующие свойства:

• P П является ли оператор идентификации I Явключен U U

• ∀ x ∈ U : P x = x .

• У нас есть прямая сумма W = U ⊕ V oplus V}. Каждый вектор x ∈ W x\в Wможет быть разложен однозначно, как x = u + v , так и где u ∈ U , v ∈ V

Диапазон и ядро проекции являются взаимодополняющими, как P Пи Q = I − P И. Оператор Q Qтакже является проекцией, поскольку диапазон и ядро P Пстановятся ядром и диапазоном Q Qи наоборот. Мы говорим P П, что это проекция вдоль V Вна U U(ядро / диапазон) и Q Qявляется проекцией вдоль U Uна V В.

Spectrum

В бесконечномерных векторных пространствах спектр проекции содержится в { 0 , 1 } виде

• ( λ I − P ) − 1 = 1 λ I + 1 λ ( λ − 1 ) P .

Только 0 или 1 могут быть собственным значением проекции, подразумевая, что P Пэто всегда положительная полуопределенная матрица. Соответствующие собственные пространства являются (соответственно) ядром и диапазоном проекции. Разложение векторного пространства на прямые суммы вообще не является уникальным. Поэтому, учитывая подпространство V В, может быть много проекций, диапазон которых (или ядро) является V В.

Если проекция нетривиальна, она имеет минимальный многочлен x 2 − x = x ( x − 1 ) , который раскладывается на различные корни и, следовательно P П, диагонализуется .

Произведение проекций

Произведение проекций вообще не является проекцией, даже если они ортогональны. Если две проекции коммутируют, то их продукт является проекцией, но обратное неверно: продукт двух не коммутирующих проекций может быть проекцией .

Если две ортогональные проекции коммутируют, то их произведение является ортогональной проекцией. Если произведение двух ортогональных проекций является ортогональной проекцией, то две ортогональные проекции коммутируют (более общо: два самосопряженных эндоморфизма коммутируют тогда и только тогда, когда их произведение является самосопряженным).

Ортогональные проекции

Когда векторное пространство W Вимеет внутреннее произведение и является полным (является гильбертовым пространством), можно использовать понятие ортогональности. Ортогональная проекция-это проекция, для которой диапазон U } Uи нулевое пространство V Вявляются ортогональными подпространствами . Таким образом, для каждого x икси y yв W В, ⟨ P x , ( y − P y ) ⟩ = ⟨ ( x − P x ) , P y ⟩ = 0 . Эквивалентно:

• ⟨ x , P y ⟩ = ⟨ P x , P y ⟩ = ⟨ P x , y ⟩

Проекция ортогональна тогда и только тогда, когда она является самосопряженной . Используя самосопряженные и идемпотентные свойства P } П, для любого x икси y yв W Вмы имеем P x ∈ U }, и

• ⟨ P x , y − P y ⟩ = ⟨ P 2 x , y − P y ⟩ = ⟨ P x , P ( I − P ) y ⟩ = ⟨ P x , ( P − P 2 ) y ⟩ = 0

где ⟨ ⋅ , ⋅ ⟩ находится внутренний продукт W В, связанный С. Поэтому P x существуют ортогональные проекции. Другое направление, а именно, что если P Портогонально, то оно самосопряженно, следует из

• ⟨ x , P y ⟩ = ⟨ P x , y ⟩ = ⟨ x , P ∗ y ⟩

для каждого x икси y yв W Втом; Таким образом P = P ∗

доказательство существования

Пусть H Хэто полное метрическое пространство с внутренним произведением, а U Uтакже замкнутое линейное подпространство H Х(и, следовательно, полное).

Для каждого x икспоследующего набора неотрицательных норм { ‖ x − u ‖ | u ∈ U } }имеется инфимум, и за счет полноты U Uон является минимальным . Мы определяем P x как точку, в U Uкоторой получен этот минимум.

Очевидно P x U, что так оно и есть . Остается показать, что P x }удовлетворяет ⟨ x − P x , P x ⟩ = 0 }и что оно линейно.

Давайте определимся a = x − P x a=x-Px. Для каждого ненулевого v {\displaystyle v} в U Uвхода выполняется следующее:

• ‖ a − ⟨ a , v ⟩ ‖ v ‖ 2 v ‖ 2 = ‖ a ‖ 2 − ⟨ a , v ⟩ 2 ‖ v ‖ 2

Определяя w = P x + ⟨ a , v ⟩ ‖ v ‖ 2 v мы видим, что ‖ x − w ‖ < ‖ x − P x ‖ если ⟨ a , v ⟩ rangle не исчезает. Так P x как был выбран минимум из указанного выше множества, то из этого следует, что ⟨ a , v ⟩ действительно исчезает. В частности, (для y = P x

Линейность вытекает из исчезновения ⟨ x − P x , v ⟩ v\rangle для каждого v ∈ U }:

• ⟨ ( x + y ) − P ( x + y ) , v ⟩ = 0
• ⟨ ( x − P x ) + ( y − P y ) , v ⟩ = 0

Принимая разность между уравнениями, которые мы имеем

• ⟨ P x + P y − P ( x + y ) , v ⟩ = 0

Но поскольку мы можем выбирать v = P x + P y − P ( x + y ) (как оно есть само по U Uсебе), это следует из этого P x + P y = P ( x + y ) . Точно так же мы имеем λ P x = P ( λ x ) }для каждого скаляра λ {лямбда .

Свойства и специальные случаи

Ортогональная проекция является ограниченным оператором . Это связано с тем, что для каждого v {\displaystyle v} вв векторном пространстве мы имеем, по неравенству Коши–Шварца:

• ‖ P v ‖ 2 = ⟨ P v , P v ⟩ = ⟨ P v , v ⟩ ≤ ‖ P v ‖ ⋅ ‖ v ‖

Таким образом ‖ P v ‖ ≤ ‖ v ‖

Для конечномерных комплексных или вещественных векторных пространств можно заменить стандартное внутреннее произведение ⟨ ⋅ , ⋅ ⟩

Формулы

Простой случай имеет место, когда ортогональная проекция находится на линии. Если u uна линии есть единичный вектор, то проекция задается внешним произведением

• P u = u u T .

(Если u uявляется комплекснозначным, транспозиция в приведенном выше уравнении заменяется эрмитовой транспозицией). Этот оператор оставляет U инвариантным , и он аннигилирует все векторы, ортогональные к u u, доказывая, что это действительно ортогональная проекция на линию, содержащую u . простой способ увидеть это-рассмотреть произвольный вектор x икскак сумму компонента на линии (т. е. проектируемого вектора, который мы ищем) и другого перпендикулярного ему, x = x ∥ + x ⊥ . Применяя проекцию, мы получаем

• P u x = u u T x ∥ + u u T x ⊥ = u ( s i g n ( u T x ∥ ) ‖ x ∥ ‖ ) + u ⋅ 0 = x ∥

по свойствам точечного произведения параллельных и перпендикулярных векторов.

Эта формула может быть обобщена на ортогональные проекции на подпространстве произвольной размерности. Пусть u 1 , … , u k }это ортонормированный базис подпространства U Uи A Одинобозначим n × k n \раз kматрицу, столбцы которой являются u 1 , … , u k , т. е. A = [ u 1 … u k ] Тогда проекция задается следующим образом:

• P A = A A T

который можно переписать как

• P A = ∑ i ⟨ u i , ⋅ ⟩ u i . .

The matrix A T A^{\mathrm {T} } is the partial isometry that vanishes on the orthogonal complement of U U and A A is the isometry that embeds U U into the underlying vector space. The range of P A is therefore the final space of A A. It is also clear that A A T is the identity operator on U U.

The orthonormality condition can also be dropped. If u 1 , … , u k } is a (not necessarily orthonormal) basis, and A

• P A = A ( A T A ) − 1 A T . .

Матрица A Одинпо-прежнему встроена U {\displaystyle U} Uв базовое векторное пространство, но больше не является изометрией в целом. Матрица ( A T A ) − 1 является "нормализующим фактором", который восстанавливает норму. Например, оператор ранга-1 u u T не является проекцией, если ‖ u ‖ ≠ 1. после деления на u T u = ‖ u ‖ 2 , мы получаем проекцию u ( u T u ) − 1 u T на подпространство, охватываемое u u.

В общем случае мы можем иметь произвольную положительно определенную матрицу D Д, определяющую внутреннее произведение ⟨ x , y ⟩ D = y † D x ,и проекция P A P_{A}задается P A x = a r g m i n y ∈ r a n g e ( A ) ‖ x − y ‖ D 2 . Затем

• P A = A ( A T D A ) − 1 A T D .

Когда пространство диапазона проекции генерируется рамкой (т. е. число генераторов больше ее размерности), формула для проекции принимает вид: P A = A A + . Здесь A + Ля^{+}расшифровывается псевдоинверсия Мура-Пенроуза . Это лишь один из многих способов построить проекционный оператор.

Если [ A B ] это неособая матрица и A T B = 0 Бявляется нулевой пространственной матрицей A Один), выполняется следующее:

• I = [ A B ] [ A B ] − 1 [ A T B T ] − 1 [ A T B T ]

= [ A B ] ( [ A T B T ] [ A B ] ) − 1 [ A T B T ]

= [ A B ] [ A T A O O B T B ] − 1 [ A T B T ]

= A ( A T A ) − 1 A T + B ( B T B ) − 1 B T

Если ортогональное условие усиливается до A T W B = A T W T B = 0 {\displaystyle A^{\mathrm {T} }WB=A^{\mathrm {T} }W^{\mathrm {T} }B=0} Внеособого, выполняется следующее:

• I = [ A B ] [ ( A T W A ) − 1 A T ( B T W B ) − 1 B T ] W .

Все эти формулы также справедливы для сложных внутренних пространств продукта, при условии, что вместо транспонирования используется сопряженная транспозиция. Более подробную информацию о суммах проекторов можно найти в Banerjee and Roy (2014). Также смотрите Banerjee (2004) [10] для применения сумм проекторов в основной сферической тригонометрии.

Косые проекции

Термин косые проекции иногда используется для обозначения неортогональных проекций. Эти проекции также используются для представления пространственных фигур на двумерных чертежах (см. наклонная проекция ), хотя и не так часто, как ортогональные проекции. В то время как вычисление установленного значения обычной регрессии наименьших квадратов требует ортогональной проекции, вычисление установленного значения регрессии инструментальных переменных требует косой проекции.

Проекции определяются их нулевым пространством и базисными векторами, используемыми для характеристики их диапазона (который является дополнением нулевого пространства). Если эти базисные векторы ортогональны нулевому пространству, то проекция является ортогональной проекцией. Когда эти базисные векторы не ортогональны нулевому пространству, проекция является косой проекцией. Пусть векторы u 1 , … , u k }образуют базис для диапазона проекции и собирают эти векторы в n × k n \раз kматрицу A Один. Диапазон и нулевое пространство являются взаимодополняющими пространствами, поэтому нулевое пространство имеет размерность n − k н-к. Отсюда следует, что ортогональное дополнение нуль-пространство имеет размерность k к. Пусть v 1 , … , v k }сформируем базис для ортогонального дополнения нулевого пространства проекции и соберем эти векторы в матрице B Б. Тогда проекция определяется по формуле

• P = A ( B T A ) − 1 B T . .

Это выражение обобщает приведенную выше формулу для ортогональных проекций. Поиск проекции с внутренним продуктом

Пусть V Вэто векторное пространство (в данном случае плоскость), охватываемое ортогональными векторами u 1 , u 2 , ⋯ , u p }. Пусть y yбудет вектор. Можно определить проекцию y yна V Вкак

• proj V ⁡ y = y ⋅ u j u j ⋅ u j u j

где j j' S подразумевают обозначение суммы Эйнштейна . Вектор y yможет быть записан в виде ортогональной суммы, такой что y = proj V ⁡ y + z }иногда обозначается как y ^ {\шляпа {y}}. Существует теорема в линейной алгебре, которая утверждает z } зет, что это самое короткое расстояние от y yдо V Ви обычно используется в таких областях, как машинное обучение.

Канонические формы

Любая проекция P = P 2 на векторное пространство размерности d днад полем является диагонализуемой матрицей, так как ее минимальный полином делится x 2 − x , который расщепляется на отдельные линейные факторы. Таким образом существует основа, в которой P Пимеет вид

• P = I r ⊕ 0 d − r

где r Рнаходится ранг P ПВ. Вот I r I_rматрица идентичности размера r Р, и 0 d − r это нулевая матрица размера d − r д-р. Если векторное пространство является сложным и снабжено внутренним произведением , то существует ортонормированный базис, в котором матрица P является

• P = [ 1 σ 1 0 0 ] ⊕ ⋯ ⊕ [ 1 σ k 0 0 ] ⊕ I m ⊕ 0 s } .

- куда σ 1 ≥ σ 2 ≥ … ≥ σ k > 0 }же . Целые k , s , m , }и вещественные числа σ i определяются однозначно. Заметьте это k + s + m = d }. Фактор I m ⊕ 0 s }соответствует максимальному инвариантному подпространству, на котором P Пдействует ортогональная проекция (так что сам P ортогональен тогда и только тогда k = 0 k=0, когда), а блоки σ i -соответствуют косым компонентам.

Проекции на нормированные векторные пространства

Когда базовое векторное пространство X Иксявляется (не обязательно конечномерным) нормированным векторным пространством , необходимо рассмотреть аналитические вопросы, не имеющие отношения к конечномерному случаю. Предположим, что теперь X Иксэто Банахово пространство .

Многие из алгебраических результатов, рассмотренных выше, переживают переход к этому контексту. Заданное разложение прямой суммы X Иксна дополнительные подпространства по-прежнему определяет проекцию, и наоборот. Если X Иксэто прямая сумма X = U ⊕ V , то оператор, определенный по P ( u + v ) = u }-прежнему является проекцией с диапазоном U Uи ядром V В. И это тоже понятно P 2 = P . И наоборот, если P Пэто проекция на X Икс, т. е. P 2 = P }, то это легко проверить ( 1 − P ) 2 = ( 1 − P ) . Другими словами, 1 − P }это тоже проекция. Это отношение P 2 = P подразумевает 1 = P + ( 1 − P ) }и X Иксявляется прямой суммой r a n ( P ) ⊕ r a n ( 1 − P ) .

Однако в отличие от конечномерного случая проекции вообще не должны быть непрерывными. Если подпространство U U X Иксне замкнуто в топологии нормы, то проекция на U Uне является непрерывной. Другими словами, диапазон непрерывной проекции P Пдолжен быть замкнутым подпространством. Кроме того, ядро непрерывной проекции (фактически, непрерывный линейный оператор в целом) замкнуто. Таким образом, непрерывная проекция P Пдает разложение X Иксна два взаимодополняющих замкнутых подпространства: X = r a n ( P ) ⊕ k e r ( P ) = k e r ( 1 − P ) ⊕ k e r ( P )

Обратное также имеет место, с дополнительным предположением. Предположим U U, это замкнутое подпространство X Икс. Если существует замкнутое подпространство V В, такое что X = U ⊕ V, то проекция P Пс диапазоном U Uи ядром V Внепрерывна. Это следует из теоремы о замкнутом графе . Пусть x n → x и Px n → y . Нужно это показать P x = y . Так U Uкак замкнут и { Px n } ⊂ U, y лежит внутри U U, т. е. Py = y . Кроме того, x n-Px n = (I − P ) x n → x − y . Поскольку V Взамкнут и {(I-P) x n } ⊂ V , мы имеем x − y ∈ V , т. е. P ( x − y ) = P x − P y = P x − y = 0 . , который доказывает утверждение.

Приведенный выше аргумент использует предположение, что оба U Взакрыты. В общем случае, учитывая замкнутое подпространство U U, не должно существовать дополнительного замкнутого подпространства V В, хотя для Гильбертовых пространств это всегда можно сделать, взяв ортогональное дополнение . Для банаховых пространств одномерное подпространство всегда имеет замкнутое дополнительное подпространство. Это является непосредственным следствием теоремы Хана-Банаха . Пусть U Uбудет линейный пролет u u. По Хану-Банаху существует ограниченный линейный функционал φ , такой что φ (u ) = 1 . Оператор P ( x ) = φ ( x ) u u}удовлетворяет P 2 = P P^{2}=P, т. е. это проекция. Ограниченность φ \varphi подразумевает непрерывность P P} П и поэтому ker ⁡ ( P ) = ran ⁡ ( I − P ) operatorname {ker} (P)=\operatorname {ran} (I-P)} \operatorname {ker} (P)=\operatorname {ran} (I-P)}является замкнутым комплементарным подпространством U .

Приложения и дополнительные соображения

Проекции (ортогональные и другие) играют важную роль в алгоритмах для некоторых задач линейной алгебры:

• QR-разложение (см. преобразование домохозяев и разложение Грама-Шмидта);
• Сингулярное разложение
• Редукция к форме Гессенберга (первый шаг во многих Алгоритмы на собственные значения)
• Линейная регрессия
• Проективные элементы матричных алгебр используются при построении некоторых K-групп в Операторная K-теория

Как указывалось выше, проекции являются частным случаем идемпотентов. Аналитически ортогональные проекции являются некоммутативными обобщениями характеристических функций . Идемпотенты используются при классификации, например, полупростых алгебр, в то время как теория мер начинается с рассмотрения характеристических функций измеримых множеств. Поэтому, как можно себе представить, проекции очень часто встречаются в контекстных операторных алгебрах . В частности, алгебра фон Неймана порождается его полной решеткой проекций.

Обобщения

В более общем случае, учитывая отображение между нормированными векторными пространствами T : V → W ,,, можно аналогично попросить, чтобы эта карта была изометрией на ортогональном дополнении ядра: это ( ker ⁡ T ) ⊥ → W Wбудет изометрия (сравните частичную изометрию ); в частности, она должна быть на. Случай ортогональной проекции - это когда W является подпространством V. В Римановой геометрии это используется в определении погружения Римана .

Смотрите также

• Центрирующая матрица, которая является примером проекционной матрицы.
• Ортогонализация
• Инвариантное подпространство
• Свойства трассировки
• Алгоритм проекции дикстры для вычисления проекции на пересечение множеств
• Гармоничные фигуры

Ссылки

• Banerjee, Sudipto; Roy, Anindya (2014), линейная алгебра и матричный анализ для статистики, тексты в статистической науке (1-е изд.), Chapman and Hall/CRC,
• Dunford, N.; Schwartz, J. T. (1958). Линейные Операторы, Часть I: Общая Теория . Interscience.
• /matrixanalysis.com/

Пруф

• .cs.mtsu.edu/
• /youtu.be/qxxo-a9snhw
• /youtu.be/osh80YCg_GM

∗ -Умножение Ю (Обьёмно-временное)