Правило 72
Не путать с 72-летним правилом .
В области финансов правило 72, правило 70 и правило 69.3 являются методами оценки времени удвоения инвестиций. Номер правила (например, 72) делится на процент процента за период (обычно лет), чтобы получить приблизительное количество периодов, необходимых для удвоения. Хотя научные калькуляторы и электронные таблицы программ имеют функции, чтобы найти точное время удвоения, правила полезны для умственных расчетов и когда только базовый калькулятор доступен.
Эти правила применяются к экспоненциальному росту и поэтому используются для сложных процентов, а не для простых расчетов процентов. Их можно также использовать для спада для того чтобы получить время halving. Выбор числа является главным образом вопросом предпочтения: 69 является более точным для непрерывного сложения, в то время как 72 хорошо работает в ситуациях общих интересов и легче делится. Существует ряд вариаций правил, которые повышают точность. Для периодического компаундирования точное время удвоения для процентной ставки r процентов за период составляет
- t = ln ( 2 ) ln ( 1 + r / 100 ) ≈ 72 r
где t-количество требуемых периодов. Приведенную выше формулу можно использовать не только для расчета времени удвоения. Если вы хотите узнать время утроения, например, замените константу 2 в числителе на 3. В качестве другого примера, если вы хотите знать, сколько периодов требуется, чтобы начальное значение увеличилось на 50%, замените константу 2 на 1.5.
Использование правила для оценки периодов компаундирования[править]
Чтобы оценить количество периодов, необходимых для удвоения первоначальной инвестиции, разделите наиболее удобное "правило-количество" на ожидаемый темп роста, выраженный в процентах.
- Например, если вы должны были инвестировать $100 со смешанным процентом по ставке 9% годовых, правило 72 дает 72/9 = 8 лет, необходимых для инвестиций на сумму $200; точный расчет дает ln(2) /ln(1+0.09) = 8.0432 года.
Аналогично, чтобы определить время, необходимое для того, чтобы ценность денег уменьшилась вдвое с заданной скоростью, разделите количество правил на эту скорость.
- Чтобы определить момент, когда покупательная способность денег уменьшится вдвое, финансисты делят количество правил на уровень инфляции . Таким образом , при инфляции 3,5%, использующей правило 70, должно пройти приблизительно 70/3.5 = 20 лет, чтобы стоимость единицы валюты уменьшилась вдвое .
- Для оценки влияния дополнительных сборов на финансовую политику (например, сборов и расходов по взаимным фондам , сборов за загрузку и расходы по переменным инвестиционным портфелям универсального страхования жизни) разделите 72 на размер сбора. Например, если универсальная жизненная политика взимает ежегодную комиссию в размере 3% сверх стоимости базового инвестиционного фонда, то общая стоимость счета будет сокращена до 1/2 за 72 / 3 = 24 года, а затем до всего лишь 1/4 стоимости за 48 лет, по сравнению с проведением точно таких же инвестиций вне политики.
Выбор правила[править]
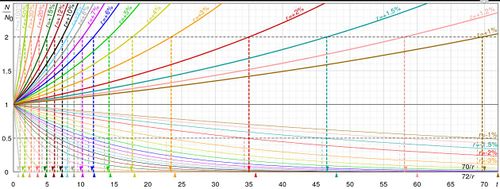
Значение 72 является удобным выбором числителя, так как имеет много малых делителей : 1, 2, 3, 4, 6, 8, 9, и еще 12. Он обеспечивает хорошее приближение для однолетнего смешивания, и для смешивать на типичных тарифах (от 6% до 10%). Эти приближения менее точны при более высоких процентных ставках.
Для непрерывного смешивания, 69 дает точные результаты для любого курса. Это связано с тем, что ln (2) составляет около 69,3%; см. Вывод ниже. Поскольку ежедневное смешивание достаточно близко к непрерывному смешиванию, для большинства целей 69, 69.3 или 70 лучше, чем 72 для ежедневного смешивания. Для более низких годовых ставок, чем те, что указаны выше, 69.3 также будет более точным, чем 72. для более высоких годовых ставок 78 является более точным.

История[править]
Ранняя ссылка на это правило содержится в книге "Сумма арифметики" (Венеция, 1494 год. ВОЛС. 181, n. 44) Луки Пачоли (1445-1514). Он представляет правило в дискуссии, касающейся оценки времени удвоения инвестиций, но не выводит или объясняет правило, и поэтому предполагается, что правило предшествует Пачоли на некоторое время.
A voler sapere ogni quantità a tanto per 100 l'anno, in quanti anni sarà tornata doppia tra utile e capitale, tieni per regola 72, a mente, il quale sempre partirai per l'interesse, e quello che ne viene, in tanti anni sarà raddoppiato. Esempio: Quando l'interesse è a 6 per 100 l'anno, dico che si parta 72 per 6; ne vien 12, e in 12 anni sarà raddoppiato il capitale. (курсив наш).
В приблизительном переводе:
Желая узнать о каком-либо капитале, при данном годовом проценте, через сколько лет он удвоится, прибавляя проценты к капиталу, имейте в виду, как правило, [число] 72, которое вы всегда будете делить на проценты, и каковы результаты, в течение которых он будет удвоен. Пример: когда процент составляет 6 процентов в год, я говорю, что один делит 72 на 6; 12 результатов, и через 12 лет капитал будет удвоен.
Корректировки для повышения точности[править]
Для более высоких ставок более крупный числитель был бы лучше (например, для 20%, используя 76, чтобы получить 3,8 года, было бы только около 0,002, где использование 72, чтобы получить 3,6, было бы около 0,2). Это происходит потому, что, как и выше, правило 72 является только приближением, которое является точным для процентных ставок от 6% до 10%. Для каждого трехпроцентного пункта вдали от 8% значение 72 может быть скорректировано на 1.
- t ≈ 72 + ( r − 8 ) / 3 r
или для того же результата, но проще:
- t ≈ 70 + ( r − 2 ) / 3 r
- t ≈ 69.3 r + 0.33
Правило E-M[править]
Правило Эккарта-Макхейла второго порядка (правило E-M) обеспечивает мультипликативную коррекцию для Правила 69.3, что очень точно для ставок от 0% до 20%. Правило 69.3 обычно является точным только при самом низком конце процентных ставок, от 0% до примерно 5%. Чтобы вычислить приближение E-M, умножьте правило 69.3 результата на 200/(200-r ) следующим образом:
- t ≈ 69.3 r × 200 200 − r
Например, если процентная ставка составляет 18%, то правило 69,3 гласит t = 3,85 лет. Правило E-M умножает это на 200/(200-18), давая время удвоения 4,23 года, где фактическое время удвоения с этой скоростью составляет 4,19 года. (Таким образом, правило E-M дает более близкое приближение, чем правило 72.)
Чтобы получить аналогичную поправку для Правила 70 или 72, один из числителей можно установить, а другой скорректировать, чтобы сохранить их произведение примерно одинаковым. Таким образом, правило Е-М может быть также записано как
- t ≈ 70 r × 198 200 − r
В этих вариантах мультипликативная поправка становится 1 соответственно для r=2 и r=8, значения для которых наиболее точны правила 70 и 72.
Аналогично, аппроксимант паде третьего порядка дает более точный ответ в еще большем диапазоне r , но он имеет несколько более сложную формулу:
- t ≈ 69.3 r × 600 + 4 r 600 + r
Вывод[править]
Периодическое компаундирование[править]
Для периодического компаундирования , будущее значение дается мимо:
- F V = P V ⋅ ( 1 + r ) t
где P V ФОТОЭЛЕКТРИЧЕСТВОтекущая стоимость- t {\displaystyle t} тэто количество периодов времени, и r {\displaystyle r} Робозначает процентную ставку за период времени.
Будущее значение удваивается по сравнению с настоящим значением, если выполняется следующее условие:
- ( 1 + r ) t = 2
Это уравнение легко решается для t } т:
- ln ( ( 1 + r ) t ) = ln 2 t ln ( 1 + r ) = ln 2 t = ln 2 ln ( 1 + r )
Простая перестановка показывает:
- ln 2 ln ( 1 + r ) = ( ln 2 r ) ( r ln ( 1 + r ) )
Если r мало, то ln (1 + r ) приблизительно равно r (это первый член в ряду Тейлора ). То есть последний термин растет медленно, когда r {\displaystyle r} Рблизок к нулю.
Вызывая этот последний член f ( r ), функция f ( r ) , как показано, является точной в приближении t тдля небольшой, положительной процентной ставки, когда r = .08 }(см. Вывод ниже). f ( .08 ) ≈ 1.03949 \приблизительно 1.03949}, и мы поэтому приблизительное время t ткак:
- t = ( ln 2 r ) f ( .08 ) ≈ .72 r
Написано в процентах:
- .72 r = 72 100 r {\displaystyle {\frac {.72}{r}}={\frac {72}{100r}}}
Эта аппроксимация увеличивает точность по мере того, как сложение интереса становится непрерывным (см. Вывод ниже). 100 r {\displaystyle 100r} Рпишется в процентах .
Для того чтобы получить более точные корректировки, представленные выше, отмечается, что ln ( 1 + r ) ,это более близко аппроксимируется r − r 2 2(используя второй член в ряду Тейлора ). 0.693 r − r 2 / 2 }затем может быть дополнительно упрощено приближениями Тейлора:
- 0.693 r − r 2 / 2 = 69.3 R − R 2 / 200 = 69.3 R 1 1 − R / 200 ≈ 69.3 ( 1 + R / 200 ) R = 69.3 R + 69.3 200 = 69.3 R + 0.34 end{массив}
Замена "R" в R/200 на третьей строке с 7.79 дает 72 на числителе. Это показывает, что правило 72 является наиболее точным для периодически составленных интересов около 8%.
В качестве альтернативы правило E-M получается, если непосредственно используется приближение Тейлора второго порядка.
Непрерывное смешивание[править]
Непрерывное компаундирование
Для непрерывного компаундирования вывод является более простым и дает более точное правило:
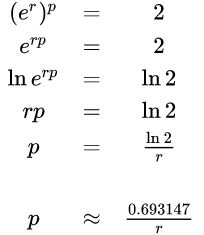
Смотрите также[править]
- Экспоненциальный рост
- Временная ценность денег
- Интерес
- Скидка
- Правило 16
- Правило третье (статистика)
- Хозяйственное мыло 72%
- 72 (число)