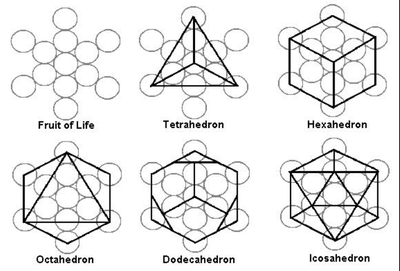
Платоновы тела

Материал из wikixw
Перейти к навигации Перейти к поиску

Атомная структура содержит ВСЕ пять Платоновых тел. Все частоты в атомной структуре построены на октавах (степень числа 2 – 2n) но додекаэдально – икосаэдрально - тетраэдральный контур (ДИТк) дополнительно построен с использованием ИСТИННОГО правила золотого сечения. Также «построен» и контур Генератора который взаимодействует («принимает») Программы «СветЛ». Теперь ответим на вопрос: где центральный кубик (см рис. 15) «обедает» кем и чем он энергетически обеспечивается? Базой для ПОСТРОЕНИЯ центрального кубика являются сегодня ещё октавы (привезены эбровской системой и ненавязчиво внедрённые):

16 22 28 32 50 54 64 66 68 72 78 88 96 112 118 122 124 128.

Диапазоны[править]

16 22 28 32 50 54 64 – материальный мир

66 68 72 – Мозг:

78 88 96 112 118 122 124 – все виды контроля.

Октава 128 – такт обменных процессов задаётся коллайдером Земли. БЕЗ ТАКТА мы имеем мёртвую материю. Относительно такта СОЗДАН Мозг зрение слух и прочее. Относительно такта на 127 октаве созданы гравитация трубки связи (и удержания) Планет спутников Солнца. Октава 128 – это МАКСИМАЛЬНАЯ октава существующей (интервентской) Системы Управления.

Эфир[править]

Все платоновы тела - источник определённого эфира - Теплород , Флогистон.

Математических действий сложение , умножение и т. д. бесчисленное множество .
Тривия это обьединение всех наук .

В геометрии платоново твердое тело представляет собой выпуклый правильный многогранник в трехмерном евклидовом пространстве. Быть правильным многогранником означает, что грани являются конгруэнтными (идентичными по форме и размеру) правильными многоугольниками (все углы совпадают и все ребра совпадают), и одинаковое количество граней встречается в каждой вершине.Таких многогранников всего пять:

Тетраэдр 4

*

Куб

*

Октаэдр 8

Геометры изучали платоновы твердые тела в течение тысяч лет. Они названы в честь древнегреческого философа Платона, который в одном из своих диалогов "Тимей" выдвинул гипотезу о том, что классические элементы были сделаны из этих правильных твердых тел.

Выпуклости - вершины излучают , а впадины поглощают энергию .Горы излучают ,например пирамиды в Египте воду . а океан поглощает.

История[править]

Платоновская твердотельная модель Солнечной системы Кеплера из Mysterium Cosmographicum (1596)

Платоновы твердые тела известны с древности. Было высказано предположение, что некоторые резные каменные шары, созданные людьми позднего неолита Шотландии, представляют эти формы; однако эти шары имеют округлые выступы, а не многогранные, количество выступов часто отличается от количества вершин платоновых тел, нет шара, чьи выступы соответствуют 20 вершинам платоновых тел.додекаэдр, и расположение выступов не всегда было симметричным.

Древние греки широко изучали платоновы твердые тела. Некоторые источники (например, Прокл) приписывают Пифагору их открытие. Другие свидетельства свидетельствуют о том, что он, возможно, был знаком только с тетраэдром, кубом и додекаэдром и что открытие октаэдра и икосаэдра принадлежит Теэтету, современнику Платона. В любом случае, Теэтет дал математическое описание всех пяти и, возможно, был ответственен за первое известное доказательство того, что других выпуклых правильных многогранников не существует.

Платоновы твердые тела занимают видное место в философии Платона, их тезки. Платон писал о них в диалоге "Тимей " около 360 г. до н.э., в котором он связал каждый из четырех классических элементов (земля, воздух, вода и огонь) с обычным твердым телом. Земля ассоциировалась с кубом, воздух - с октаэдром, вода - с икосаэдром, а огонь - с тетраэдром. У этих ассоциаций было интуитивное обоснование: жар огня ощущается острым и колющим (как маленькие тетраэдры). Воздух состоит из октаэдра; его крошечные компоненты настолько гладкие, что его едва можно почувствовать. Вода, икосаэдр, вытекает из руки, когда ее берут, как будто она сделана из крошечных шариков. Шестигранник (куб), напротив, является несферическим твердым телом, представляющим "землю". Эти неуклюжие маленькие твердые частицы заставляют грязь крошиться и ломаться, когда ее поднимают, в отличие от плавного потока воды.Более того, считалось, что то, что куб является единственным правильным твердым телом, которое мозаично евклидово пространство, вызывает твердость Земли.

Присвоение элементам в Mysterium Cosmographicum Кеплера

О пятом платоновом твердом теле, додекаэдре, Платон туманно заметил: "... бог использовал [его] для расположения созвездий на всем небе". Аристотель добавил пятый элемент, aithēr (эфир на латыни, "эфир" на английском языке) и постулировал, что небеса состоят из этого элемента, но он не был заинтересован в сопоставлении его с пятым твердым телом Платона.[4]

Евклид полностью математически описал платоновы твердые тела в "Элементах", последняя книга (книга XIII) которой посвящена их свойствам. Предложения 13-17 в книге XIII описывают построение тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в таком порядке. Для каждого твердого тела Евклид находит отношение диаметра описанной сферы к длине ребра. В предложении 18 он утверждает, что больше не существует выпуклых правильных многогранников. Андреас Шпайзер отстаивал мнение, что построение пяти правильных твердых тел является главной целью дедуктивной системы, канонизированной в Элементах. Большая часть информации в книге XIII, вероятно, почерпнута из работы Теэтета.

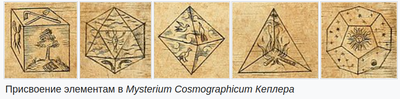
В 16 веке немецкий астроном Иоганн Кеплер попытался связать пять известных в то время внеземных планет с пятью платоновыми твердыми телами. В книге "Mysterium Cosmographicum", опубликованной в 1596 году, Кеплер предложил модель Солнечной системы, в которой пять твердых тел были расположены внутри друг друга и разделены рядом вписанных и описанных сфер. Кеплер предположил, что соотношение расстояний между шестью известными в то время планетами можно понять в терминах пяти платоновых тел, заключенных в сферу, которая представляла орбиту Сатурна. Каждая из шести сфер соответствовала одной из планет (Меркурий, Венера, Земля, Марс, Юпитер и Сатурн). Твердые тела были упорядочены, самым внутренним из которых был октаэдр, за которым следовали икосаэдр, додекаэдр, тетраэдр и, наконец, куб, тем самым определяя структуру солнечной системы и соотношение расстояний между планетами с помощью платоновых тел. В конце концов от первоначальной идеи Кеплера пришлось отказаться, но из его исследований вышли три закона орбитальной динамики, первым из которых было то, чтоорбиты планет представляют собой эллипсы, а не окружности, что меняет ход физики и астрономии. Он также открыл твердые тела Кеплера, которые представляют собой два невыпуклых правильных многогранника.

Декартовы координаты[править]

Для платоновых тел с центром в начале координат простые декартовы координаты вершин приведены ниже. Греческая буква φ используется для обозначения золотого сечения

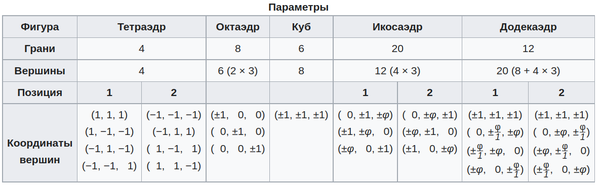
2/1 + √ 5 ≈ 1.6180.

Координаты тетраэдра, додекаэдра и икосаэдра задаются в двух положениях, так что каждое из них может быть выведено из другого: в случае тетраэдра путем изменения всех координат знака (центральная симметрия) или, в других случаях, путем обмена двумя координатами (отражение относительно любогоиз трех диагональных плоскостей).

Эти координаты показывают определенные отношения между платоновыми телами: вершины тетраэдра представляют половину вершин куба, как {4,3} или Узел CDel 1.pngCDel 4.pngУзел CDel.pngCDel 3.pngУзел CDel.png, один из двух наборов из 4 вершин в двойных положениях, как h {4,3} или Узел CDel h.pngCDel 4.pngУзел CDel.pngCDel 3.pngУзел CDel.png. Оба положения тетраэдра образуют составной звездчатый октаэдр.

Координаты икосаэдра связаны с двумя чередующимися наборами координат неоднородного усеченного октаэдра, t {3,4} или Узел CDel 1.pngCDel 3.pngУзел CDel 1.pngCDel 4.pngУзел CDel.png, также называемого тупым октаэдром, как s {3,4} или Узел CDel h.pngCDel 3.pngУзел CDel h.pngCDel 4.pngУзел CDel.png, и видны в соединении двух икосаэдров.

Восемь вершин додекаэдра являются общими с кубом. Завершение всех ориентаций приводит к составлению пяти кубов.

Комбинаторные свойства[править]

Выпуклый многогранник является платоновым твердым телом тогда и только тогда, когда

все его грани являются конгруэнтными выпуклыми правильными многоугольниками,

ни одна из его граней не пересекается, кроме как на их краях, и
в каждой из его вершин встречается одинаковое количество граней.
Поэтому каждое платоновское твердое тело может быть обозначено символом {p, q}, где

p - число ребер (или, что эквивалентно, вершин) каждой грани, и

q - количество граней (или, что эквивалентно, ребер), которые встречаются в каждой вершине.
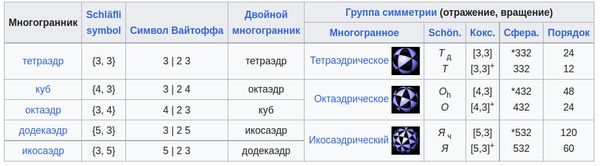
Символ {p, q}, называемый символом Шлефли, дает комбинаторное описание многогранника. Символы Шлефли пяти платоновых тел приведены в таблице ниже.

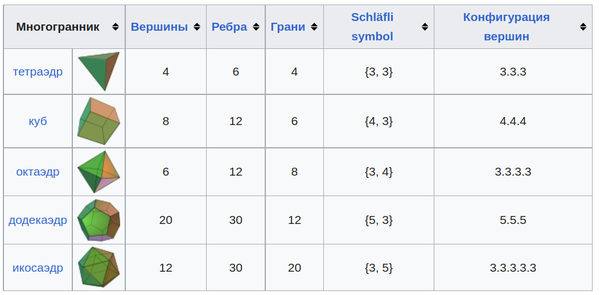
Вся другая комбинаторная информация об этих телах, такая как общее количество вершин (V), ребер (E) и граней (F), может быть определена из p и q. Поскольку любое ребро соединяет две вершины и имеет две смежные грани, мы должны иметь: 

pF=2E=qV.\,}pF=2E=qV.\,
Другая связь между этими значениями задается формулой Эйлера:
V-E+F=2.\,}V-E+F=2.\,
Это можно доказать многими способами. Вместе эти три отношения полностью определяют V, E и F:
V={\frac {4p}{4-(p-2)(q-2)}},\quad E={\frac {2pq}{4-(p-2)(q-2)}},\quad F={\frac {4q}{4-(p-2)(q-2)}}.}V= {\ frac {4p} {4-(p-2) (q-2)}},\quad E={\frac {2pq}{4- (p-2) (q-2)}},\quad F= {\frac {4q}{4-(p-2)(q-2)}}.
Замена p и q приводит к замене F и V, оставляя E неизменным. Для геометрической интерпретации этого свойства см. § Двойные многогранники.

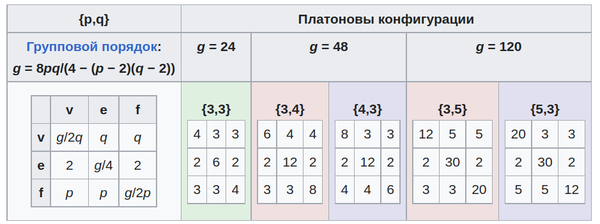
Как конфигурация[править]

Элементы многогранника могут быть выражены в матрице конфигурации. Строки и столбцы соответствуют вершинам, ребрам и граням. Диагональные числа говорят о том, сколько каждого элемента встречается во всем многограннике. Недиагональные числа говорят о том, сколько элементов столбца встречается в элементе строки или в элементе строки. Двойные пары многогранников имеют свои конфигурационные матрицы, повернутые на 180 градусов друг от друга.

Классификация[править]

Классический результат состоит в том, что существует только пять выпуклых правильных многогранников. Два приведенных ниже общих аргумента демонстрируют, что может существовать не более пяти платоновых твердых тел, но позитивная демонстрация существования любого данного твердого тела — это отдельный вопрос, который требует явной конструкции.

Геометрическое доказательство[править]

Следующий геометрический аргумент очень похож на аргумент, приведенный Евклидом в элементах:

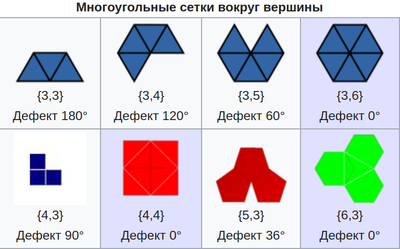
Для вершины требуется не менее 3 граней и дефект угла. Дефект угла 0 ° заполнит евклидову плоскость обычной плиткой. По теореме Декарта число вершин равно 720°/дефект.

Каждая вершина твердого тела должна быть вершиной по крайней мере для трех граней.

В каждой вершине твердого тела общее количество углов между смежными гранями между их соответствующими смежными сторонами должно быть строго меньше 360°. Величина, меньшая 360°, называется дефектом угла.
Правильные многоугольники с шестью или более сторонами имеют только углы 120 ° или более, поэтому общей гранью должен быть треугольник, квадрат или пятиугольник. Для этих различных форм граней выполняется следующее:
Треугольные грани
Каждая вершина правильного треугольника равна 60 °, поэтому фигура может иметь три, четыре или пять треугольников, сходящихся в вершине; это тетраэдр, октаэдр и икосаэдр соответственно.
Квадратные грани
Каждая вершина квадрата равна 90 °, поэтому возможно только одно расположение с тремя гранями в вершине, кубе.
Пятиугольные грани
Каждая вершина равна 108 °; опять же, возможно только одно расположение трех граней в вершине, додекаэдр.
В целом это дает пять возможных платоновых тел.

Топологическое доказательство[править]

Чисто топологическое доказательство может быть сделано с использованием только комбинаторной информации о твердых телах. Ключевым моментом является наблюдение Эйлера о том, что V − E + F = 2, и тот факт, что pF = 2 E = qV, где p обозначает количество ребер каждой грани, а q - количество ребер, встречающихся в каждой вершине. Объединяя эти уравнения, получаем уравнение
Ортографические проекции и диаграммы Шлегеля с гамильтоновыми циклами вершин пяти платоновых тел – только октаэдр имеет эйлерову траекторию или цикл, расширяя свой путь пунктиром
{\frac {2E}{q}}-E+{\frac {2E}{p}}=2.
Простая алгебраическая манипуляция тогда дает
{1 \over q}+{1 \over p}={1 \over 2}+{1 \over E}.}{1 \над q}+{1 \над p}={1 \над 2}+{1 \над E}.
Поскольку E строго положительно, мы должны иметь
{\frac {1}{q}}+{\frac {1}{p}}>{\frac {1}{2}}.}{\frac {1}{q}}+{\frac {1}{p}}>{\frac {1}{2}}.

Используя тот факт, что p и q оба должны быть не менее 3, можно легко увидеть, что существует только пять возможностей для {p, q}:

{3, 3}, {4, 3}, {3, 4}, {5, 3}, {3, 5}.

Геометрические свойства[править]

Углы[править]

Существует ряд углов, связанных с каждым платоновым твердым телом. Двугранный угол - это внутренний угол между любыми двумя плоскостями граней. Двугранный угол, θ, твердого тела {p, q} задается формулой 

\sin \left({\frac {\theta }{2}}\right)={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}.}{\displaystyle \sin \left({\frac {\theta }{2}}\right)={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\справа)}}.}
Иногда это удобнее выразить в терминах касательной через
\tan \left({\frac {\theta }{2}}\right)={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{h}}\right)}}.}{\displaystyle \tan \left({\frac {\theta }{2}}\right)={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{h}}\справа)}}.}
Величина h (называемая числом Кокстера) равна 4, 6, 6, 10 и 10 для тетраэдра, куба, октаэдра, додекаэдра и икосаэдра соответственно.

Угловой недостаток в вершине многогранника равен разнице между суммой углов граней в этой вершине и 2 π. Дефект δ в любой вершине платоновых тел {p,q} равен 

\delta =2\pi -q\pi \left(1-{2 \over p}\right).}{\displaystyle \delta =2\pi -q\pi \left(1-{2 \над p}\right).}
По теореме Декарта это равно 4 π, деленному на количество вершин (т.е. Общий дефект во всех вершинах равен 4 π).

Трехмерным аналогом плоского угла является телесный угол. Телесный угол Ω в вершине платонова тела задается через двугранный угол через

\Omega =q\theta -(q-2)\pi .\,}{\displaystyle \Omega =q\theta -(q-2)\pi .\,}

Это следует из формулы сферического избытка для сферического многоугольника и того факта, что вершинная фигура многогранника {p, q} является правильным q-угольником.

Телесный угол грани, вытянутой из центра платонова твердого тела, равен телесному углу полной сферы (4 π стерадиана), деленному на количество граней. Это равно угловому недостатку его двойственного.

Различные углы, связанные с платоновыми твердыми телами, приведены в таблице ниже. Числовые значения телесных углов приведены в стерадианах. Константа φ =

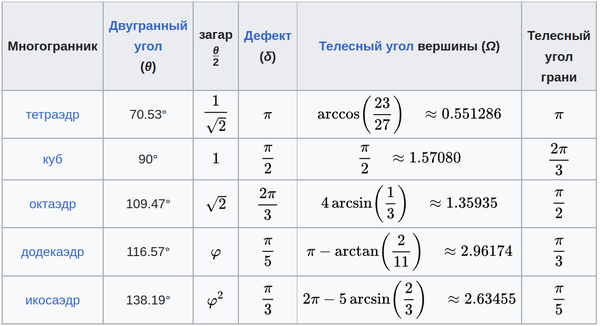
2/1 + √ 5 - золотое сечение.

Радиусы, площадь и объем[править]

Другим достоинством регулярности является то, что все платоновы твердые тела обладают тремя концентрическими сферами:

ограниченная сфера, проходящая через все вершины, средняя сфера, которая касается каждого ребра в средней точке ребра, и вписанная сфера, которая касается каждой грани в центре грани.

Радиусы этих сфер называются радиусом окружности, средним радиусом и внутренним радиусом. Это расстояния от центра многогранника до вершин, срединных точек ребер и центров граней соответственно. Радиус окружности R и радиус r твердого тела {p, q} с длиной ребра a задаются формулой
{\begin{aligned}R&={\frac {a}{2}}\tan \left({\frac {\pi }{q}}\right)\tan \left({\frac {\theta }{2}}\right)\\[3pt]r&={\frac {a}{2}}\cot \left({\frac {\pi }{p\lefd}}}\end{выровнено}}}
где θ - двугранный угол. Средний радиус ρ задается
 \rho ={\frac {a}{2}}\cos \left({\frac {\pi }{p}}\right)\,{\csc }{\biggl (}{\frac {\pi }{h}}{\biggr )}})}}
где h - величина, используемая выше при определении двугранного угла (h = 4, 6, 6, 10 или 10). Отношение окружного радиуса к внутреннему радиусу симметрично по p и q:
{\frac {R}{r}}=\tan \left({\frac {\pi }{p}}\right)\tan \left({\frac {\pi }{q}}\right)={\frac {\sqrt {{\csc ^{2}}{\Bigl (}{\frac {\theta }{2}}{\Bigr )}-{\frac {\alpha }{\Bigr )}}}.}
Площадь поверхности A платонова твердого тела {p, q} легко вычисляется как площадь правильного p-угольника, умноженная на число граней F. Это:
A={\biggl (}{\frac {a}{2}}{\biggr )}^{2}Fp\cot \left({\frac {\pi }{p}}\right).}{\displaystyle A={\biggl (}{\frac {a}{2}}{\biggr )}^{2}Fp\cot \left({\frac {\pi }{p}}\right).}
Объем вычисляется как F, умноженный на объем пирамиды, основанием которой является правильный p-угольник, а высотой - радиус r. Это,
V={\frac {1}{3}}rA.}{\displaystyle V={\frac {1}{3}}rA.}
В следующей таблице перечислены различные радиусы платоновых тел вместе с их площадью поверхности и объемом. Общий размер фиксируется путем принятия длины ребра a равной 2.

Константы φ и ξ в приведенном выше задаются 

\varphi =2\cos {\pi \over 5}={\frac {1+{\sqrt {5}}}{2}},\qquad \xi =2\sin {\pi \over 5}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}={\sqrt {3-\varphi }}.}{\displaystyle \varphi =2\cos {\pi \over 5}={\frac {1+{\sqrt {5}}}{2}},\ qquad \xi =2\sin {\pi \более 5}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}={\ sqrt {3-\varphi }}.}
Среди платоновых тел додекаэдр или икосаэдр можно рассматривать как наилучшее приближение к сфере. Икосаэдр имеет наибольшее количество граней и наибольший двугранный угол, он наиболее плотно охватывает вписанную в него сферу, а его отношение площади поверхности к объему наиболее близко к отношению сферы того же размера (т.Е. Либо той же площади поверхности, либо того же объема). Додекаэдр, с другой стороны, имеет наименьший угловой дефект, наибольший телесный угол вершины, и он больше всего заполняет свою описанную сферу.

Точка в пространстве[править]

Для произвольной точки в пространстве платонова тела с радиусом окружности R, расстояния до центра тяжести платонова тела и его n вершин равны L и d i соответственно, и 

S_{[n]}^{(2m)}={\frac {1}{n}}\sum _{i=1}^{n}d_{i}^{2m}}{\displaystyle S_{[n]}^{(2m)}={\frac {1}{n}}\sum _{i=1}^{n}d_{i}^{2m}},

мы имеем[7] 

{\begin{aligned}S_{[4]}^{(2)}=S_{[6]}^{(2)}=S_{[8]}^{(2)}=S_{[12]}^{(2)}=S_{[20]}^{(2)}&=R^{2}+L^{2},\\[4px]S_{[4]}^{(4)}=S_{[6]}^{(4)}=S_{[8]}^{(4)}=S_{[12]}^{(4)}=S_{[20]}^{(4)}&=\left(R^{2}+L^{2}\right)^{2}+{\frac {4}{3}}R^{2}L^{2},\\{aligned}}}

Для всех пяти платоновых твердых тел мы имеем 

S_{[n]}^{(4)}+{\frac {16}{9}}R^{4}=\left(S_{[n]}^{(2)}+{\frac {2}{3}}R^{2}\right)^{2}.}
Если di - расстояния от n вершин платонова тела до любой точки на его описанной сфере, то[7]
4\left(\sum _{i=1}^{n}d_{i}^{2}\right)^{2}=3n\sum _{i=1}^{n}d_{i}^{4}.}

Собственность Руперта[править]

Говорят, что многогранник P обладает свойством Руперта, если многогранник того же или большего размера и той же формы, что и P, может проходить через отверстие в P.[8] Все пять платоновых тел обладают этим свойством.

Симметрия[править]

Двойные многогранники[править]

Каждый многогранник имеет двойной (или "полярный") многогранник с взаимозаменяемыми гранями и вершинами. Двойственным каждого платонова твердого тела является другое платоновское твердое тело, так что мы можем расположить пять твердых тел в двойственные пары.

Двойные соединения

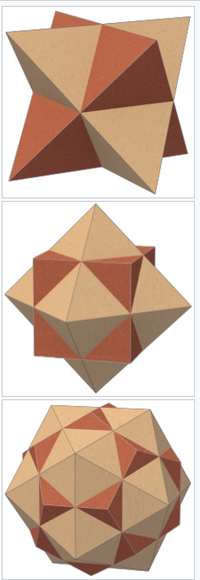
Тетраэдр самодуальен (т.е. его двойственным является другой тетраэдр).

Куб и октаэдр образуют двойственную пару.
Додекаэдр и икосаэдр образуют двойственную пару.
Если многогранник имеет символ Шлефли {p, q}, то его двойственный имеет символ {q, p}. Действительно, каждое комбинаторное свойство одного платонова твердого тела может быть интерпретировано как другое комбинаторное свойство двойственного.

Можно построить двойной многогранник, приняв вершины двойственного за центры граней исходной фигуры. Соединение центров смежных граней в оригинале образует ребра двойственного и, таким образом, меняет местами количество граней и вершин при сохранении количества ребер.

В более общем смысле, можно дуализировать платоновское твердое тело относительно сферы радиуса d, концентрической с твердым телом. Радиусы (R, ρ, r) твердого тела и его двойственного (R *, ρ *, r *) связаны 

d^{2}=R^{\ast }r=r^{\ast }R=\rho ^{\ast }\rho .}d ^ {2}= R^ {\ast } r= r^ {\ast } R = \rho ^{\ast } \ rho .
Дуализация относительно средней сферы (d = ρ) часто удобна, потому что средняя сфера имеет одинаковое отношение к обоим многогранникам. Взятие d2 = Rr дает двойное твердое тело с одинаковым радиусом окружности и радиусом (т. е. R * = R и r * = r).

Группы симметрии[править]

В математике понятие симметрии изучается с понятием математической группы. Каждому многограннику соответствует группа симметрии, представляющая собой множество всех преобразований (евклидовых изометрий), которые оставляют многогранник инвариантным. Порядок группы симметрии - это число симметрий многогранника. Часто различают полную группу симметрии, которая включает отражения, и правильную группу симметрии, которая включает только вращения.

Группы симметрии платоновых тел представляют собой особый класс трехмерных точечных групп, известных как полиэдральные группы. Высокая степень симметрии платоновых тел может быть интерпретирована несколькими способами. Самое главное, что все вершины каждого твердого тела эквивалентны под действием группы симметрии, так же как ребра и грани. Говорят, что действие группы симметрии транзитивно на вершинах, ребрах и гранях. Фактически, это еще один способ определения регулярности многогранника: многогранник является регулярным тогда и только тогда, когда он однороден по вершинам, однороден по краям илицо-однородное.

Существует только три группы симметрии, связанные с платоновыми телами, а не пять, поскольку группа симметрии любого многогранника совпадает с группой симметрии его двойника. Это легко увидеть, изучив конструкцию двойного многогранника. Любая симметрия оригинала должна быть симметрией двойственного и наоборот. Три многогранные группы:

тетраэдрическая группа T, октаэдрическая группа O (которая также является группой симметрии куба) и группа икосаэдров I (которая также является группой симметрии додекаэдра).

Порядки собственных (вращающихся) групп равны 12, 24 и 60 соответственно – ровно в два раза больше числа ребер в соответствующих многогранниках. Порядки полных групп симметрии снова в два раза больше (24, 48 и 120). См. (Coxeter 1973) для вывода этих фактов. Все платоновы тела, кроме тетраэдра, центрально-симметричны, что означает, что они сохраняются при отражении через начало координат.

В следующей таблице перечислены различные свойства симметрии платоновых тел. Перечисленные группы симметрии являются полными группами с подгруппами вращения, указанными в круглых скобках (аналогично для числа симметрий). Построение калейдоскопа Витхоффа - это метод построения многогранников непосредственно из их групп симметрии. Они перечислены для справки символом Вайтоффа для каждого из платоновых твердых тел.

В природе и технологии[править]

Тетраэдр, куб и октаэдр встречаются в природе в кристаллических структурах. Это ни в коем случае не исчерпывает числа возможных форм кристаллов. Однако среди них нет ни правильного икосаэдра, ни правильного додекаэдра. Одна из форм, называемая пиритоэдром (названа по группе минералов, для которых она типична), имеет двенадцать пятиугольных граней, расположенных по тому же образцу, что и грани правильного додекаэдра. Грани пиритоэдра, однако, не являются регулярными, поэтому пиритоэдр также не является регулярным. Аллотропы бора и многие соединения боратакие как карбид бора, включают в свои кристаллические структуры дискретные икосаэдры B12. Карборановые кислоты также имеют молекулярные структуры, приближающиеся к правильным икосаэдрам.

Икосаэдры Circogonia, вид радиолярий, по форме напоминающий правильный икосаэдр.

В начале 20-го века Эрнст Геккель описал (Haeckel, 1904) ряд видов радиолярий, некоторые скелеты которых имеют форму различных правильных многогранников. Примеры включают октаэдр Circoporus, икосаэдры Circogonia, геометрический куб и додекаэдры Circorrhegma. Формы этих существ должны быть очевидны из их названий.

Многие вирусы, такие как вирус герпеса[, имеют форму правильного икосаэдра. Вирусные структуры построены из повторяющихся идентичных белковых субъединиц, и икосаэдр - самая простая форма для сборки с использованием этих субъединиц. Используется правильный многогранник, потому что его можно построить из одного базового белка, используемого снова и снова; это экономит место в вирусном геноме.

В метеорологии и климатологии все больший интерес представляют глобальные численные модели атмосферного потока, в которых используются геодезические сетки, основанные на икосаэдре (уточненном с помощью триангуляции) вместо более часто используемой сетки долготы / широты. Это имеет преимущество в равномерно распределенном пространственном разрешении без особенностей (т. Е. полюсов) за счет несколько большей численной сложности.


Икосаэдр как часть памятника Спинозе в Амстердаме
Геометрия пространственных структур часто основана на платоновых телах. В системе MERO платоновы твердые тела используются для обозначения различных конфигураций пространственных фреймов. :Например,

2/1 

O + T относится к конфигурации, состоящей из половины октаэдра и тетраэдра.

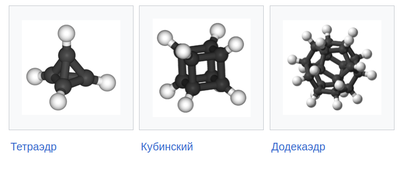
Было синтезировано несколько платоновых углеводородов, в том числе кубан и додекаэдран, а не тетраэдран.

Набор многогранных кубиков.

Платоновы твердые тела часто используются для изготовления кубиков, потому что кубики такой формы можно сделать честными. 6-сторонние кости очень распространены, но другие числа обычно используются в ролевых играх. Такие кости обычно называют dn, где n - количество граней (d8, d20 и т.д.); подробнее см. Обозначение кости.

Эти фигуры часто появляются в других играх или головоломках. Головоломки, похожие на кубик Рубика, бывают всех пяти форм – см. Волшебные многогранники.

Жидкие кристаллы с симметриями платоновых тел[править]

Для промежуточной материальной фазы, называемой жидкими кристаллами, существование таких симметрий было впервые предложено в 1981 году Х. Кляйнертом и К. Маки.]В алюминии икосаэдрическая структура была обнаружена через три года после этого Дэном Шехтманом, что принесло ему Нобелевскую премию по химии в 2011 году.

Связанные многогранники и многогранники[править]

Однородные многогранники[править]

Существуют четыре правильных многогранника, которые не являются выпуклыми, называемые многогранниками Кеплера–Пуансо. Все они имеют икосаэдрическую симметрию и могут быть получены как звездочки додекаэдра и икосаэдра.

кубооктаэдр икосидодекаэдр

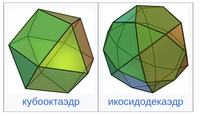
Следующими по правильности выпуклыми многогранниками после платоновых тел являются кубоктаэдр, представляющий собой выпрямление куба и октаэдра, и икосидодекаэдр, представляющий собой выпрямление додекаэдра и икосаэдра (выпрямление самодуального тетраэдра представляет собой правильный октаэдр). Они оба квазирегулярны, что означает, что они однородны по вершинам и ребрам и имеют правильные грани, но грани не все совпадают (входят в два разных класса). Они образуют два из тринадцати архимедовых тел, которые являются выпуклымиоднородные многогранники с многогранной симметрией. Их двойники, ромбический додекаэдр и ромбический триаконтаэдр, являются переходными по ребрам и граням, но их грани не являются правильными, а их вершины бывают двух типов каждая; они являются двумя из тринадцати каталонских тел.

Однородные многогранники образуют гораздо более широкий класс многогранников. Эти фигуры однородны по вершинам и имеют один или несколько типов правильных или звездчатых многоугольников для граней. К ним относятся все упомянутые выше многогранники вместе с бесконечным множеством призм, бесконечным множеством антипризм и 53 другими невыпуклыми формами.

Твердые тела Джонсона представляют собой выпуклые многогранники, которые имеют правильные грани, но не являются однородными. Среди них пять из восьми выпуклых дельтаэдров, которые имеют одинаковые правильные грани (все равносторонние треугольники), но не являются однородными. (Другими тремя выпуклыми дельтаэдрами являются платонов тетраэдр, октаэдр и икосаэдр.)

Регулярные мозаики[править]

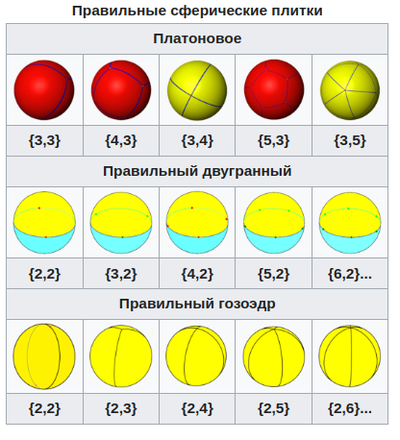
Три регулярные мозаики плоскости тесно связаны с платоновыми телами. Действительно, можно рассматривать платоновы твердые тела как регулярные мозаики сферы. Это делается путем проецирования каждого твердого тела на концентрическую сферу. Грани проецируются на правильные сферические многоугольники, которые точно покрывают сферу. Сферические разбиения предоставляют два бесконечных дополнительных набора правильных разбиений, хосоэдры, {2,n} с 2 вершинами на полюсах и лунными гранями, и двойные диэдры, {n,2} с 2 полусферическими гранями и регулярно расположенными вершинами на экваторе. Такие тесселяции были бы вырожденными в истинном трехмерном пространстве как многогранники.

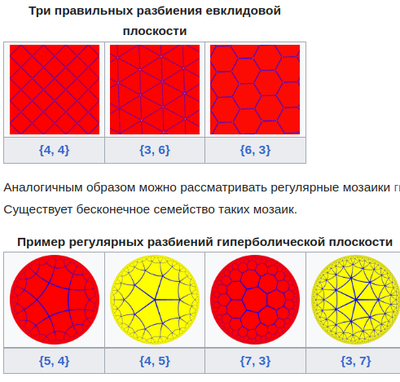
Можно показать, что каждая регулярная тесселяция сферы характеризуется парой целых чисел {p, q} с

p / 1 + вопрос / 1 > 2/1

. Аналогично, регулярная тесселяция плоскости характеризуется условием

p / 1 

+

q / 1 = 2/1 . Есть три возможности:

Аналогичным образом можно рассматривать регулярные мозаики гиперболической плоскости. Они характеризуются условием

p / 1 + вопрос / 1 < 2/1 . Существует бесконечное семейство таких мозаик.

Высшие измерения[править]

Дополнительная информация: Список правильных многогранников

Т
Количество измерений Число выпуклых правильных многогранников
0 1
1 1
2 ∞
3 5
4 6
> 4 3

В более чем трех измерениях многогранники обобщаются на многогранники, причем многомерные выпуклые правильные многогранники являются эквивалентами трехмерных платоновых тел.

В середине 19 века швейцарский математик Людвиг Шлефли открыл четырехмерные аналоги платоновых тел, называемые выпуклыми правильными 4-многогранниками. Таких фигур ровно шесть; пять аналогичны платоновым твердым телам: 5-клеточный как {3,3,3}, 16-клеточный как {3,3,4}, 600-клеточный как {3,3,5}, тессеракт как {4,3,3} и 120-клеточный как {5,3,3}, и шестой,самодвойственная 24-клеточная, {3,4,3}.

Во всех измерениях выше четырех существует только три выпуклых правильных многогранника: симплекс в виде {3,3,...,3}, гиперкуб в виде {4,3,...,3} и кросс-многогранник в виде {3,3,...,4}.[14] В трех измерениях они совпадаютс тетраэдром как {3,3}, кубом как {4,3} и октаэдром как {3,4}.

Смотри также[править]

Архимедово твердое тело * Каталонское твердое тело * Дельтаэдр * Твердое тело Джонсона * Твердое тело Голдберга * Твердые тела Кеплера * Список правильных многогранников * Куб принца Руперта * Правильные многогранники * Правильный косой многогранник * Тороидальный многогранник Геодезический купол

Читать[править]

/archive.org/details/thirteenbooksofe00eucl

Пруф[править]

/youtu.be/V1NtbzXKTTI

Источник — https://wikixw.ru/index.php?title=Платоновы_тела&oldid=65285